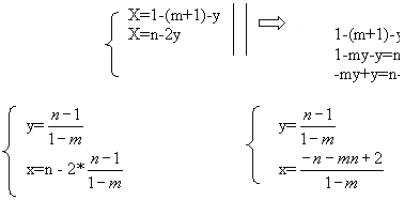Урок. «Решение уравнений с модулем и параметром. Системы уравнений с параметром Линейные уравнение с параметрами и модулем

Цель:

повторить решение систем линейных уравнений с двумя переменными
дать определение системы линейных уравнений с параметрами
научит решать системы линейных уравнений с параметрами.

Ход урока

Организационный момент
Повторение
Объяснение новой темы
Закрепление
Итог урока
Домашнее задание

2. Повторение:

I. Линейное уравнение с одной переменной:

1. Дайте определение линейного уравнения с одной переменной

[Уравнение вида ax=b, где х – переменная, а и b некоторые числа, называется линейным уравнением с одной переменной]

2. Сколько корней может иметь линейное уравнение?

[- Если а=0, b0, то уравнение не имеет решений, х

Если а=0, b=0, то х R

Если а0, то уравнение имеет единственное решение, х =

3. Выясните, сколько корней имеет уравнение (по вариантам)

II. Линейное уравнение с 2 –мя переменными и система линейных уравнений с 2- мя переменными.

1. Дайте определение линейного уравнения с двумя переменными. Приведите пример.

[Линейным уравнением с двумя переменными называются уравнения вида ах +by=с, где х и у – переменные, а, b и с – некоторые числа. Например, х-у=5]

2. Что называется решением уравнения с двумя переменными?

[Решением уравнения с двумя переменными называются пара значений переменных, обращающие это уравнение в верное равенство.]

3. Является ли пара значений переменных х = 7, у = 3 решением уравнения 2х + у = 17?

4. Что называется графиком уравнения с двумя переменными?

[Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых является решениями этого уравнения.]

5. Выясните, что представляет собой график уравнения:

[Выразим переменную у через х: у=-1,5х+3

Формулой у=-1,5х+3 является линейная функция, графиком которой служит прямая. Так как, уравнения 3х+2у=6 и у=-1,5х+3 равносильны, то эта прямая является и графиком уравнения 3х+2у=6]

6. Что является графиком уравнения ах+bу=с с переменными х и у, где а0 или b0?

[Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.]

7. Что называется решением системы уравнений с двумя переменными?

[Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство]

8. Что значит решить систему уравнений?

[Решить систему уравнений – значит найти все ее решения или доказать, что решений нет.]

9. Выясните, всегда ли имеет такая система решения и если имеет, то сколько (графическим способом).

10. Сколько решений может иметь система двух линейных уравнений с двумя переменными?

[Единственное решение, если прямые пересекаются; не имеет решений, если прямые параллельны; бесконечно много, если прямые совпадают]

11. Каким уравнением обычно задается прямая?

12. Установите связь между угловыми коэффициентами и свободными членами:

I вариант:

у=-х+2
y= -x-3,

k 1 = k 2 , b 1 b 2, нет решений;

II вариант:

y=-х+8
y=2x-1,

k 1 k 2 , одно решение;

III вариант:

y=-x-1
y=-x-1,

k 1 = k 2 , b 1 = b 2, много решений.

Вывод:

Если угловые коэффициенты прямых являющихся графиками этих функций различны, то эти прямые пересекаются и система имеет единственное решение.
Если угловые коэффициенты прямых одинаковы, а точки пересечения с осью у различны, то прямые параллельны, а система не имеет решений.
Если угловые коэффициенты и точки пересечения с осью у одинаковы, то прямые совпадают и система имеет бесконечно много решений.

На доске таблица, которую постепенно заполняет учитель вместе с учениками.

III. Объяснение новой темы.

Определение: Система вида

A 1 x+B 1 y=C
A 2 x+B 2 y=C 2

где A 1, A 2, B 1 ,B 2, C 1 C 2 – выражения, зависящие от параметров, а х и у – неизвестные, называется системой двух линейных алгебраических уравнений с двумя неизвестными в параметрах.

Возможны следующие случаи:

1) Если , то система имеет единственное решение

2) Если , то система не имеет решений

3) Если , то система имеет бесконечно много решений.

IV. Закрепление

Пример 1.

При каких значениях параметра а система

2х - 3у = 7
ах - 6у = 14

а) имеет бесконечное множество решений;

б) имеет единственное решение

Ответ:

а) если а=4, то система имеет бесконечное множество решений;

б) если а 4, то решение единственное.

Пример 2.

Решите систему уравнений

x+(m+1)y=1
x+2y=n

Решение: а) , т.е. при m1 система имеет единственное решение.

б) , т.е. при m=1 (2=m+1) и n1 исходная система решений не имеет

в) , при m=1 и n=1 система имеет бесконечно много решений.

Ответ: а) если m=1 и n1, то решений нет

б) m=1 и n=1, то решение бесконечное множество

у - любое
x=n-2y

в) если m1 и n - любое, то

Пример 3.

ах-3ау=2а+3
х+ау=1

Решение: Из II уравнения найдем х=1-ау и подставим в I уравнение

а(1-ау)-3ау=2а+3

а-а 2 у-3ау=2а+3

А 2 у-3ау=а+3

А(а+3)у=а+3

Возможны случаи:

1) а=0. Тогда уравнение имеет вид 0*у=3 [у ]

Следовательно, при а=0 система не имеет решений

2) а=-3. Тогда 0*у=0.

Следовательно, у . При этом х=1-ау=1+3у

3) а0 и а-3. Тогда у=-, х=1-а(-=1+1=2

Ответ:

1) если а=0, то (х; у)

2) если а=-3, то х=1+3у, у

3) если а 0 и а?-3, то х=2, у=-

Рассмотрим II способ решения системы (1).

Решим систему (1) методом алгебраического сложения: вначале умножим первое уравнение системы на В 2, второе на – В 1 и сложим почленно эти уравнения, исключив, таким образом, переменную у:

Т.к. А 1 В 2 -А 2 В 1 0, то х =

Теперь исключим переменную х. Для этого умножим первое уравнение системы (1) на А 2 , а второе на – А 1 , и оба уравнения сложим почленно:

А 1 А 2 х +А 2 В 1 у=А 2 С 1
-А 1 А 2 х-А 1 В 2 у=-А 1 С 2
у(А 2 В 1 -А 1 В 2)=А 2 С 1 -А 1 С 2

т.к. А 2 В 1 -А 1 В 2 0 у =

Для удобства решения системы (1) введем обозначения:

- главный определитель

Теперь решение системы (1) можно записать с помощью определителей:

Приведенные формулы называют формулами Крамера.

Если , то система (1) имеет единственное решение: х=; у=

Если , или , , то система (1) не имеет решений

Если , , , , то система (1) имеет бесконечное множество решений.

В этом случае систему надо исследовать дополнительно. При этом, как правило, она сводится к одному линейному уравнению. В случае часто бывает удобно исследовать систему следующим образом: решая уравнение , найдем конкретные значения параметров или выразим один из параметров через остальные и подставим эти значения параметров в систему. Тогда получим систему с конкретными числовыми коэффициентами или с меньшим числом параметров, которую надо и исследовать.

Если коэффициенты А 1 , А 2 , В 1 , В 2 , системы зависят от нескольких параметров, то исследовать систему удобно с помощью определителей системы.

Пример 4.

Для всех значений параметра а решить систему уравнений

(а+5)х+(2а+3)у=3а+2
(3а+10)х+(5а+6)у=2а+4

Решение: Найдем определитель системы:

= (а+5)(5а+6) – (3а+10) (2а+3)= 5а 2 +31а+30-6а 2 -29а-30=-а 2 +2а=а(2-а)

= (3а+2) (5а+6) –(2а+4)(2а+3)=15а 2 +28а+12-4а 2 -14а-12=11а 2 +14а=а(11а+14)

=(а+5) (2а+4)-(3а+10)(3а+2)=2а 2 +14а+20-9а 2 -36а-20=-7а 2 -22а=-а(7а+22)

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.

Задачи:

Образовательные : научить решать некоторые виды уравнений уравнений модулями и параметрами;
Развивающие : развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
Воспитательные : воспитывать самостоятельность и умение преодолевать трудности.

Оборудование: наглядный материал для устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное оборудование урока.

Структура урока:

Повторение изученного материала (устный счёт).
Изучение нового материала.
Закрепление изученного материала.
Итог урока.
Домашнее задание.

ХОД УРОКА

1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»

1) «Уравнения, содержащие модуль»

Абсолютной величиной или модулем числа a называется число a , если a > 0, число – a , если a < 0, нуль, если a = 0. Или

Из определения следует, что | a | > 0 и | a | > a для всех a € R .
Неравенство | x | < a , (если a > 0) равносильно двойному неравенству – a < х < a .
Неравенство | x | < a , (если a < 0) не имеет смысла, так как | х | >0.
Неравенство | x | > a , (если a > 0) равносильно двум неравенствам
Неравенство | x | > a , (если a < 0) справедливо для любого х € R.

2) «Решение уравнений с параметрами»

Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.

а) определить множество допустимых значений неизвестного и параметров;

б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения.

2. Устные упражнения

1. Решить уравнение | x – 2 | = 5; Ответ : 7; – 3

| x – 2 | = – 5; Ответ : решения нет

| x – 2 | = х + 5; Ответ : решения нет; 1,5

| x – 2 | = | x + 5 |; Ответ : решения нет; – 1,5; решения нет; – 1,5;

2. Решить уравнение: | x + 3 | + | y – 2 | = 4;

Расcмотрим четыре случая

{	x + 3 > 0	{	x > – 3
	y – 2 > 0		y > 2
	x + 3 + y – 2 = 4		y = – x + 3

{	x + 3 > 0	{	x > – 3
	y – 2 < 0		y < 2
	x + 3 – y + 2 = 4		y = x + 1

{	x + 3 < 0	{	x < – 3
	y + 2 > 0		y > – 2
	– x – 3 – y – 2 = 4		y = x + 9

{	x + 3 < 0	{	x < – 3
	y + 2 < 0		y < – 2
	– x – 3 – y – 2 = 4		y = – x – 9

В результате мы получаем квадрат, центр которого (–3; 2), а длина диагонали равна 8, причем диагонали параллельны осям координат.

Из наглядных соображений можно сделать вывод: что уравнение вида | х + a | + | у + b | = с ; задает на плоскости квадрат с центром в точке (– а ; – b ), диагоналями параллельными осям OX и ОУ, и длина каждой диагонали равна 2с . Ответ : (– 3; 2).

2. Решить уравнение aх = 1

Ответ : если a = 0, то нет решения; если a = 0, то х = 1/ a

3. Решить уравнение (а 2 – 1) х = а + 1.

Решение .

Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи:

1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения

2) а = – 1; получаем ОX = О, и очевидно х – любое.

1
3) если а = + 1, то х = –––
а – 1

Ответ:
если а = – 1, то х – любое;
если а = 1, то нет решения;

1
если а = + 1 , то х = –––
а – 1

3. Решения примеров (из вариантов С)

1. При каком значении параметра р уравнение | х 2 – 5х + 6 | + | х 2 – 5х + 4 | = р имеет четыре корня.

Рассмотрим функцию у = | х 2 – 5х + 6 | + | х 2 – 5х + 4 |

Так как х 2 – 5х + 6 = (х – 2)(х – 3) и х 2 – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой

1 2 3 4 х

Числовая прямая при этом разбивает на 5 промежутков

{	x < 1	{	x < 1
	y = x 2 – 5x + 6 + x 2 – 5x + 4		y = 2x 2 – 10x + 10

{	1 < x < 2	{	1 < x < 2
	y = x 2 – 5x + 6 – x 2 + 5x – 4		y = 2

{	2 < x < 3	{	2 < x <3
	y = – 2x 2 + 10x – 10		y = – x 2 + 5x – 6 – x 2 + 5x – 4

{	3 < x < 4	{	3 < x < 4
	y = 2		y = x 2 – 5x + 6 – x 2 + 5x – 4

{	x > 4	{	x > 4
	y = 2x 2 – 10x + 10		y = x 2 – 5x + 6 + x 2 –5x + 4

Для случая 3) х 0 = – b | 2a = 2, y 0 = 25: 2 + 25 – 10 = 2,5

Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x 2 + 10x – 10.

Построим график функции, заданной равенством

Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 < а < 2,5

Ответ : при 2 < а < 2,5

4. Самостоятельная работа по уровням

1 уровень

1. Решить уравнение х 2 – | x | = 6
2. При каких целых значениях а имеет единственное решение уравнение ах 2 – (а + 1) + а 2 + а = 0?

2 уровень

1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10
а –12) х 2 + 2 = 2(12 – а ) имеет два различных корня?

3 уровень

1. Решить уравнение | x – 5 | – | 2x + 3| = 10
2. Найти все значениях параметра а, при которых уравнение (а – 12) х 2 + 2 = 2(12 – а ) имеет два различных корня?

5. Итог урока

1. Определение модуля.
2. Что значит решить уравнение с параметром?

6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012

«Линейное уравнение с двумя переменными» - Равенство, содержащее две переменные, называется уравнением с двумя переменными. -Что называется уравнением с двумя переменными? Приведите примеры. -Какое уравнение с двумя переменными называется линейным? Линейное уравнение с двумя переменными. Определение: Алгоритм доказательства, что данная пара чисел является решением уравнения:

«Решение показательных уравнений» - Сведение к одному основанию. Вынесение за скобки. Т. Виета. Графический способ. Показательным уравнением называют уравнение, содержащее переменную в показателе степени. Решение показательных уравнений. Устная работа. ab+ac=a(b+c). Степени. 2.Решить уравнение: Свойство. Виды и способы решения показательных уравнений.

«Графический способ решения уравнений» - Ответ: один корень, х=-1. Два корня. Решить графически уравнение (х+1)/(х-2)=2. Построить график функции y=x?+6x+8. Практикум по решению уравнений графическим способом Подготовка к зачету. Построить графики функций. Построить график функции y=(x+1)/(x-2). 1. Перенесем 8 в правую часть уравнения. Корней нет.

«Решение целых уравнений» - «Уравнения, в которых скопом Корни, степень, неравенств бездна. Три великих математика. Удачи в дальнейшем изучении методов решения уравнений. Осевая симметрия присуща большинству видов растений и животных. Центральная. В животном мире 2 вида симметрии. Диктант. Осевая. Определите методы решения уравнений.

«Уравнения с логарифмами» - Логарифмические уравнения. Реши устно уравнения. Формулы преобразования логарифмов. Уравнение. Определение. Таблицы логарифмов. Определение логарифма. Определение и свойства логарифма. Логарифмическая линейка. Функция. Наушники или колонки. Область определения. Подходы к решению. Решить уравнение. Гимназия.

«Иррациональные уравнения» - На контроль д/з выполнили: №419 (в,г) Сафиуллина, №418(в,г) Кульмухаметов, №420(в,г)Шагеев. 2 урок Решение систем уравнений. Урок 1 Тема: Решение иррациональных уравнений. 1.Какие из следующих уравнений являются иррациональными: Цели: Познакомить учащихся с решениями некоторых видов иррациональных уравнений.

Всего в теме 49 презентаций

Как говорили древние философы «Мудрость – это любовь к знаниям, а любовь – это мера всех вещей». «Мера» на латинском языке - «modulus», от него и произошло слово «модуль». И сегодня мы с вами поработаем с уравнениями, содержащими модуль. Надеюсь, у нас все получится, и в конце урока мы с вами станем мудрее.

Скачать:

Предварительный просмотр:

Пирогова Татьяна Николаевна г. Таганрог МОУ СОШ № 10.

Тема: «Решение уравнений с модулем и параметром»

10 класс, занятие элективного курса «Свойства функции».

План урока.

Мотивация.
Актуализация знаний.
Решение линейного уравнения с модулем разными способами.
Решение уравнений содержащих модуль под модулем.
Исследовательская работа по определению зависимости количества корней уравнения

| | х| - а |= в от значений а и в.

Рефлексия.

Ход урока.

Мотивация. Как говорили древние философы «Мудрость – это любовь к знаниям, а любовь – это мера всех вещей». «Мера» на латинском языке - «modulus», от него и произошло слово «модуль». И сегодня мы с вами поработаем с уравнениями, содержащими модуль. Надеюсь, у нас все получится, и в конце урока мы с вами станем мудрее.

Актуализация знаний. Итак, вспомним, что мы уже знаем о модуле .

Определение модуля. Модулем действительного числа – называется само число, если оно неотрицательно и противоположное ему число, если оно отрицательно.

Геометрический смысл модуля. Модуль действительного числа а равен расстоянию от начала отсчета до точки с координатой а на числовой прямой.

– a 0 a

|– a | = | a | | a | x

Геометрический смысл модуля разности величин. Модуль разности величин | а – в | - это расстояние между точками с координатами а и в на числовой прямой,

Т.е. длина отрезка [ а в ]

1) Если a b 2) Если a > b

a b b a

S = b – a S = a – b

3) Если a = b , то S = a – b = b – a = 0

Основные свойства модуля

Модуль числа есть число неотрицательное, т.е. | x | ≥ 0 для любого x
Модули противоположных чисел равны, т.е. | x | = |– x | для любого x
Квадрат модуля равен квадрату подмодульного выражения, т.е. | x | 2 = x 2 для любого x

4. Модуль произведения двух чисел равен произведению модулей сомножителей, т.е.| a b | = | a | · | b |

5. Если знаменатель дроби отличен от нуля, то модуль дроби равен частному от деления модуля числителя на модуль знаменателя, т.е. при b ≠ 0

6. Для равенства любых чисел a и b справедливы неравенства :

| | a | – | b | | ≤ | a + b | ≤ | a | + | b |

| | a | – | b | | ≤ | a – b | ≤ | a | + | b |

График модуля у = | х | - прямой угол с вершиной в начале координат, стороны которого являются биссектрисами 1 и 2 квадрантов.
Как построить графики функций? у = | х –4|, у = | х +3|, у = | х –3|, у = | х | + 1 ,
у = | х | – 3, у = | х | – 5, у = | х – 3 | + 3, у = | х – 3 | – 2, у = | х + 2 | – 5. у = || х| – а |

Пример. Решить уравнение .

Способ 1. Метод раскрытия модулей по промежуткам.

Способ 2. Непосредственное раскрытие модуля.

Если модуль числа равен 3, то это число 3 или -3.

Способ 3 . Использование геометрического смысла модуля.

Необходимо найти на числовой оси такие значения х, которые удалены от 2 на расстояние, равное 3.

Способ 4. Возведение обеих частей уравнения в квадрат.

Здесь используется свойство модуля

И то, что обе части уравнения неотрицательные.

Способ 5. Графическое решение уравнения .

Обозначим. Построим графики функций и :

Абсциссы точек пересечения графиков дадут корни





2 -1 0 1 2 3

2 -1 0 1 2 3 4 5




2 -1 0 1 2 3

2 -1 0 1 2 3 4 5

Самостоятельная работа

решите уравнения:

| х – 1| = 3

| х – 5| = 3

| х –3| = 3

| х + 3| = 3

| х + 5| = 3

(-2; 4)

(2; 8)

(0; 6)

(-6; 0)

(-8;-2)

А теперь добавьте в условия еще один модуль и решите уравнения:

| | х| – 1| = 3

| | х| –5| = 3

| | х | – 3| = 3

| | х | + 3| = 3

| | х | + 5| = 3

(нет корней)

Итак, сколько корней может иметь уравнение вида | | х | – а |= в? От чего это зависит?

Исследовательская работа по теме

«Определение зависимости количества корней уравнения | | х | – а |= в от а и в »

Проведем работу по группам, с использованием аналитического, графического и геометрического способов решения.

Определим, при каких условиях данное уравнение имеет 1 корень, 2 корня, 3 корня, 4 корня и не имеет корней.

1 группа (по определению)

2 группа (используя геометрический смысл модуля)

3 группа (используя графики функций)

А > 0
	1 группа	2 группа	3 группа
Нет корней	в в ≥ 0 в + а	в в ≥ 0 а + в	в в ≥ 0 в а
ровно один корень	в > 0 и в + а = 0	в > 0 и в + а = 0	в > 0 и в = – а
ровно два корня	в > 0 и в + а > 0 – в + а	в > 0 и в + а > 0 – в + а	в > 0 и в > \| а \|
ровно три корня	в > 0 и – в + а = 0	в > 0 и – в + а = 0	в > 0 и в = а
ровно четыре корня	в > 0 и – в + а >0	в > 0 и – в + а >0	в > 0 и в а

Сравните результаты, сделайте общий вывод и составьте общую схему.

Конечно, необязательно эту схему запоминать . Главное в проведенном нами исследовании было – увидеть эту зависимость, используя разные методы , и теперь повторить свои рассуждения при решении таких уравнений нам будет уже несложно.

Ведь решение задания с параметром всегда подразумевает некоторое исследование.

Решение уравнений с двумя модулями и параметром.

1. Найти значения р, х| – р – 3| = 7 имеет ровно один корень.

Решение: | | х| – (р + 3)| = 7

р +3= -7, р = -10. Или геометрически

р + 3 – 7 р + 3 р + 3+7 р + 3+7=0, р = -10

7 7 по схеме уравнение такого вида имеет ровно один корень, если в = – а, где в =7, а = р +3

2. Найти значения р, при каждом из которых уравнение | | х| – р – 6| = 11 имеет ровно два корня.

Решение: | | х| – (р + 6)| = 11 геометрически

Р + 6 – 11 р + 6 р + 6+11 р + 6-11 р р + 6+11>0, р > -17

11 11

по схеме уравнение такого вида имеет ровно два корня, если в + а > 0 и – в + а где в =11, а = р +6. -17р 5.

3. Найти значения р, при каждом из которых уравнение | | х| – 4 р | = 5 р –9 имеет ровно четыре корня.

Решение: по схеме уравнение такого вида имеет ровно четыре корня, если

0р –9 р, р > и р

т.е. 1 р 9.

Ответ: 1 р 9.

4 . . Найти значения р, при каждом из которых уравнение | | х| – 2 р | = 5 р +2 не имеет корней. Решение: 5 р +2 р +2 =0 и –2 р >0, или 5 р +2 >0 и 5 р +2 р.

р р = –0,4, или р > – 0,4 и р . Ответ : р

5. При каких значениях параметра р уравнение | | х –4 | – 3| + 2 р = 0 имеет три корня. Найти эти корни.

Преобразуем уравнение к виду:

| | х –4 | – 3|= – 2 р .

По схеме уравнение такого вида имеет три корня,

если –2 р =3>0,

Т.е. р = –1,5.

|| х –4|–3| = 3,

| х –4|=0, х = 4,

|| х –4|=6, х = –2, х =10.

Ответ: при р = –1,5 уравнение имеет три корня: х 1 = –2, х 2 = 4, х 3 =10.

Подведение итогов урока. Рефлексия.

Скажите, какие бы вы выделили главные слова урока? (Модуль, параметр)

Что мы сегодня повторили? (Определение модуля, геометрический смысл модуля числа и разности чисел, свойства модуля, разные способы решения уравнений)

Что мы сегодня делали?

Домашнее задание.

Уравнения с параметрами

Математика – единственный совершенный метод, позволяющий провести самого себя за нос. Альберт Эйнштейн

№ 1 Найдите все значения a, при каждом из которых уравнение x² + (a + 5)² = |x + a + 5| + |x – a -5| имеет ровно три корня.

РЕШЕНИЕ Уравнение не изменится, если заменить x числом –x . Следовательно, уравнение имеет чётное число ненулевых решений. Значит, три решения уравнения имеет только тогда, когда одно из них 0. Поставим x = 0 .

Получим: (a + 5)² = 2|a + 5|

Откуда a + 5 = 0 или |a + 5| = 2.

Если a + 5 = 0, уравнение принимает вид x² = 2|x| и имеет ровно три решения: -2, 0, 2. Из a + 5 = 0 получаем: a = -5. Если |a +5| = 2, уравнение принимает вид x² + 4 = |x + 2| + |x – 2|.

2 уравнение принимает вид x² - 2x + 4 = 0 и не имеет решений. Аналогично решений нет при x Ответ: a = -5. " width="640"

При -2 ≤ x ≤ 2 уравнение имеет единственное решение 0. При x 2 уравнение принимает вид x² - 2x + 4 = 0 и не имеет решений. Аналогично решений нет при x Ответ: a = -5.

№ 2

Найдите все значения параметра a, при котором уравнение f(x) = |2a + 5|x

имеет 6 решений, где f -- чётная периодическая функция, с периодом Т = 2, определённая на всей числовой прямой, причём f(x) = ax², если 0≤x≤1 .

РЕШЕНИЕ Если а = 0, функция f(x) тождественно равна нулю, и её график имеет с прямой y = 5x единственную общую точку.

0, то 9а = -25. Положительных решений нет. Следовательно, случай а 0 невозможен. " width="640"

Пусть а = 0, (рис. 1). Решение х = 0 есть при всех а. Нужно ещё ровно пять решений. Единственный возможный случай показан на рисунке: прямая проходит через точку (5 ; а). Составим уравнение |2a + 5| ∙ 5 = a. Так как а 0, то 9а = -25. Положительных решений нет. Следовательно, случай а 0 невозможен.

№ 3 Найдите все значения а, при каждом из которых функция f(x) = x² - 3|x - a²| - 5x имеет более двух точек экстремума. РЕШЕНИЕ При х ≥ а² f (x) = x² - 8x + 3a², поэтому график функции есть часть параболы с ветвями, направленными вверх, и осью симметрии х = 4.