Tangent planes play a big role in geometry. The construction of tangent planes is of practical importance, since their presence makes it possible to determine the direction of the normal to the surface at the point of contact. This problem is widely used in engineering practice. Tangent planes are also used to construct outlines of geometric figures bounded by closed surfaces. Theoretically, planes tangent to a surface are used in differential geometry to study the properties of a surface in the region of the point of contact.
Basic concepts and definitions
The plane tangent to the surface should be considered as the limiting position of the secant plane (by analogy with the line tangent to the curve, which is also defined as the limiting position of the secant).
A plane tangent to a surface at a given point on the surface is the set of all straight lines - tangents drawn to the surface through a given point.
In differential geometry it is proven that all tangents to a surface drawn at an ordinary point are coplanar (belonging to the same plane).
Let's find out how to draw a straight line tangent to the surface. The tangent t to the surface β at a point M specified on the surface (Fig. 203) represents the limiting position of the secant l j intersecting the surface at two points (MM 1, MM 2, ..., MM n) when the intersection points coincide (M ≡ M n , l n ≡ l M). Obviously (M 1, M 2, ..., M n) ∈ g, since g ⊂ β. From the above, the following definition follows: tangent to a surface is a straight line tangent to any curve belonging to the surface.
Since the plane is defined by two intersecting straight lines, to define a plane tangent to the surface at a given point, it is enough to draw two arbitrary lines belonging to the surface (preferably simple in shape) through this point, and construct tangents to each of them at the point of intersection of these lines . The constructed tangents uniquely determine the tangent plane. A visual representation of drawing a plane α tangent to the surface β at a given point M is given in Fig. 204. This figure also shows the normal n to the surface β.

The normal to the surface at a given point is a straight line perpendicular to the tangent plane and passing through the point of tangency.
The line of intersection of the surface with a plane passing through the normal is called the normal section of the surface. Depending on the type of surface, the tangent plane can have either one or many points (line) with the surface. The line of tangency can at the same time be the line of intersection of the surface with the plane.
There are also cases when there are points on the surface at which it is impossible to draw a tangent to the surface; such points are called singular. As an example of singular points, one can cite the points belonging to the return edge of the torso surface, or the point of intersection of the meridian of the surface of revolution with its axis, if the meridian and the axis do not intersect at right angles.
Types of touch depend on the nature of the surface curvature.
Surface curvature
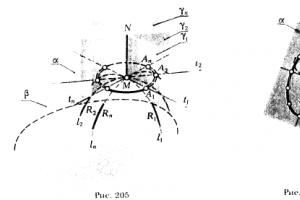
Issues of surface curvature were studied by the French mathematician F. Dupin (1784-1873), who proposed a visual way to depict changes in the curvature of normal sections of a surface.
To do this, in the plane tangent to the surface under consideration at point M (Fig. 205, 206), segments equal to the square roots of the values of the corresponding radii of curvature of these sections are laid on the tangents to the normal sections on both sides of this point. A set of points - the ends of segments define a curve called Dupin's indicatrix. The algorithm for constructing the Dupin indicatrix (Fig. 205) can be written:
1. M ∈ α, M ∈ β ∧ α β;
2. = √(R l 1), = √(R l 2),..., = √(R l n)
where R is the radius of curvature.
(A 1 ∪ A 2 ∪ ... ∪ A n) is the Dupin indicatrix.

If the Dupin indicatrix of a surface is an ellipse, then the point M is called elliptic, and the surface is called a surface with elliptic points(Fig. 206). In this case, the tangent plane has only one common point with the surface, and all lines belonging to the surface and intersecting at the point under consideration are located on one side of the tangent plane. Examples of surfaces with elliptical points are: a paraboloid of revolution, an ellipsoid of revolution, a sphere (in this case, the Dupin indicatrix is a circle, etc.).
When drawing a tangent plane to the torso surface, the plane will touch this surface along a straight generatrix. The points on this line are called parabolic, and the surface is a surface with parabolic points. Dupin's indicatrix in this case is two parallel lines (Fig. 207*).
In Fig. 208 shows a surface consisting of points in which
* A second-order curve - a parabola - under certain conditions can split into two real parallel lines, two imaginary parallel lines, two coinciding lines. In Fig. 207 we are dealing with two real parallel lines.
Any tangent plane intersects the surface. Such a surface is called hyperbolic, and the points belonging to it are hyperbolic points. Dupin's indicatrix in this case is a hyperbole.
A surface, all points of which are hyperbolic, has the shape of a saddle (oblique plane, single-sheet hyperboloid, concave surfaces of revolution, etc.).
One surface can have points of different types, for example, on the torso surface (Fig. 209) point M is elliptical; point N is parabolic; point K is hyperbolic.
In the course of differential geometry it is proven that normal sections in which the curvature values K j = 1/ R j (where R j is the radius of curvature of the section under consideration) have extreme values are located in two mutually perpendicular planes.
Such curvatures K 1 = 1/R max. K 2 = 1/R min are called the main values, and the values H = (K 1 + K 2)/2 and K = K 1 K 2 are, respectively, the average curvature of the surface and the total (Gaussian) curvature of the surface at the point under consideration. For elliptic points K > 0, hyperbolic points K
Specifying a tangent plane to a surface on a Monge diagram
Below, using specific examples, we will show the construction of a plane tangent to a surface with elliptic (example 1), parabolic (example 2) and hyperbolic (example 3) points.
EXAMPLE 1. Construct a plane α tangent to the surface of revolution β with elliptic points. Let's consider two options for solving this problem: a) point M ∈ β and b) point M ∉ β
Option a (Fig. 210).
The tangent plane is determined by two tangents t 1 and t 2 drawn at point M to the parallel and meridian of the surface β.
The projections of the tangent t 1 to the parallel h of the surface β will be t" 1 ⊥ (S"M") and t" 1 || x axis The horizontal projection of the tangent t" 2 to the meridian d of the surface β passing through the point M will coincide with the horizontal projection of the meridian. To find the frontal projection of the tangent t" 2, the meridional plane γ(γ ∋ M) is transferred to the position γ by rotating around the axis of the surface β 1, parallel to the plane π 2. In this case, point M → M 1 (M" 1, M" 1). The projection of the tangent t" 2 rarr; t" 2 1 is determined by (M" 1 S"). If we now return the plane γ 1 to its original position, then the point S" will remain in place (as belonging to the axis of rotation), and M" 1 → M" and the frontal projection of the tangent t" 2 will be determined (M" S")
Two tangents t 1 and t 2 intersecting at a point M ∈ β define a plane α tangent to the surface β.
Option b (Fig. 211)
To construct a plane tangent to a surface passing through a point that does not belong to the surface, one must proceed from the following considerations: through a point outside the surface consisting of elliptic points, many planes tangent to the surface can be drawn. The envelope of these surfaces will be some conical surface. Therefore, if there are no additional instructions, then the problem has many solutions and in this case reduces to drawing a conical surface γ tangent to a given surface β.
In Fig. 211 shows the construction of a conical surface γ tangent to the sphere β. Any plane α tangent to the conical surface γ will be tangent to the surface β.
To construct projections of the surface γ from points M" and M" we draw tangents to the circles h" and f" - the projections of the sphere. Mark touch points 1 (1" and 1"), 2 (2" and 2"), 3 (3" and 3") and 4 (4" and 4"). Horizontal projection of a circle - the line of tangency of the conical surface and the sphere is projected into [ 1"2"] To find the points of the ellipse into which this circle will be projected onto the frontal plane of projections, we will use the parallels of the sphere.
In Fig. 211 in this way the frontal projections of points E and F (E" and F") are determined. Having a conical surface γ, we construct a tangent plane α to it. The nature and sequence of graphic


The constructions that need to be done for this are given in the following example.
EXAMPLE 2 Construct a plane α tangent to the surface β with parabolic points
As in Example 1, we consider two solutions: a) point N ∈ β; b) point N ∉ β
Option a (Fig. 212).
A conical surface refers to surfaces with parabolic points (see Fig. 207.) A plane tangent to a conical surface touches it along a rectilinear generatrix. To construct it, it is necessary:
1) through a given point N draw a generator SN (S"N" and S"N");
2) mark the point of intersection of the generatrix (SN) with the guide d: (SN) ∩ d = A;
3) will also blow to the tangent t to d at point A.
The generatrix (SA) and the tangent t intersecting it define the plane α tangent to the conical surface β at a given point N*.
To draw a plane α, tangent to the conical surface β and passing through the point N, does not belong to
* Since the surface β consists of parabolic points (except for the vertex S), the tangent plane α to it will have in common not one point N, but a straight line (SN).
pressing a given surface, it is necessary:
1) through a given point N and the vertex S of the conical surface β draw a straight line a (a" and a") ;
2) determine the horizontal trace of this straight line H a;
3) through H a draw the tangents t" 1 and t" 2 of the curve h 0β - the horizontal trace of the conical surface;
4) connect the tangent points A (A" and A") and B (B" and B") to the vertex of the conical surface S (S" and S").
The intersecting lines t 1, (AS) and t 2, (BS) determine the desired tangent planes α 1 and α 2
EXAMPLE 3. Construct a plane α tangent to the surface β with hyperbolic points.
Point K (Fig. 214) is located on the surface of the globoid (the inner surface of the ring).



To determine the position of the tangent plane α it is necessary:
1) draw a parallel to the surface β h(h", h") through point K;
2) through the point K" draw a tangent t" 1 (t" 1 ≡ h");
3) to determine the directions of the projections of the tangent to the meridional section, it is necessary to draw the plane γ through the point K and the axis of the surface, the horizontal projection t" 2 will coincide with h 0γ; to construct the frontal projection of the tangent t" 2, we first translate the plane γ by rotating it around the axis of the surface of rotation to position γ 1 || π 2. In this case, the meridional section by plane γ will align with the left outline arc of the frontal projection - semicircle g".
Point K (K", K"), belonging to the meridional section curve, will move to position K 1 (K" 1, K" 1). Through K" 1 we draw a frontal projection of the tangent t" 2 1, combined with the plane γ 1 || π 2 position and mark the point of its intersection with the frontal projection of the axis of rotation S" 1. We return the plane γ 1 to its original position, point K" 1 → K" (point S" 1 ≡ S"). The frontal projection of the tangent t" 2 is determined by the points K" and S".
Tangents t 1 and t 2 define the desired tangent plane α, which intersects the surface β along the curve l.
EXAMPLE 4. Construct a plane α tangent to the surface β at point K. Point K is located on the surface of a one-sheet hyperboloid of revolution (Fig. 215).
This problem can be solved by adhering to the algorithm used in the previous example, but taking into account that the surface of a one-sheet hyperboloid of revolution is a ruled surface that has two families of rectilinear generators, and each of the generators of one family intersects all the generators of the other family (see § 32, fig. 138). Through each point of this surface, two intersecting straight lines can be drawn - generators, which will simultaneously be tangent to the surface of a one-sheet hyperboloid of revolution.
These tangents define the tangent plane, that is, the plane tangent to the surface of a one-sheet hyperboloid of revolution intersects this surface along two straight lines g 1 and g 2. To construct projections of these lines, it is enough to carry the horizontal projection of point K and the tangents t" 1 and t" 2 to the horizontal
tal projection of the circle d" 2 - the throat of the surface of a single-sheet hyperboloid of revolution; determine points 1" and 2 at which t" 1 and t" 2 intersect one and the directing surfaces d 1. From 1" and 2" we find 1" and 2", which together with K" determine the frontal projections of the required lines.
At some point and has continuous partial derivatives at it, at least one of which does not vanish, then in the neighborhood of this point the surface defined by equation (1) will be the right surface.
In addition to the above implicit way of specifying surface can be defined obviously, if one of the variables, for example z, can be expressed in terms of the others:
There is also parametric way of assignment. In this case, the surface is determined by the system of equations:

The concept of a simple surface
More accurately, simple surface is called the image of a homeomorphic mapping (that is, a one-to-one and mutually continuous mapping) of the interior of a unit square. This definition can be given an analytical expression.
Let a square be given on a plane with a rectangular coordinate system u and v, the coordinates of the internal points of which satisfy the inequalities 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").
Example simple surface is a hemisphere. The entire sphere is not simple surface. This necessitates further generalization of the concept of surface.
A subset of space, each point of which has a neighborhood that is simple surface, called the right surface .
Surface in differential geometry
Helicoid

Catenoid
The metric does not uniquely determine the shape of the surface. For example, the metric of a helicoid and a catenoid, parameterized accordingly, coincides, that is, there is a correspondence between their regions that preserves all lengths (isometry). Properties that are preserved under isometric transformations are called internal geometry surfaces. The internal geometry does not depend on the position of the surface in space and does not change when it is bent without tension or compression (for example, when a cylinder is bent into a cone).
Metric coefficients determine not only the lengths of all curves, but also in general the results of all measurements inside the surface (angles, areas, curvature, etc.). Therefore, everything that depends only on the metric refers to internal geometry.
Normal and normal section

Normal vectors at surface points
One of the main characteristics of a surface is its normal- unit vector perpendicular to the tangent plane at a given point:
The sign of the normal depends on the choice of coordinates.
A section of a surface by a plane containing the normal (at a given point) forms a certain curve on the surface, which is called normal section surfaces. The main normal for a normal section coincides with the normal to the surface (up to sign).
If the curve on the surface is not a normal section, then its main normal forms a certain angle θ with the normal of the surface. Then the curvature k curve related to curvature k n normal section (with the same tangent) by Meunier's formula:
The coordinates of the normal unit vector for different methods of defining a surface are given in the table:
| Normal coordinates at a surface point | |
|---|---|
| implicit assignment |  |
| explicit assignment |  |
| parametric specification |  |
Curvature
For different directions at a given point on the surface, different curvature of the normal section is obtained, which is called normal curvature; it is assigned a plus sign if the main normal of the curve goes in the same direction as the normal to the surface, or a minus sign if the directions of the normals are opposite.
Generally speaking, at every point on a surface there are two perpendicular directions e 1 and e 2, in which the normal curvature takes minimum and maximum values; these directions are called main. The exception is the case when the normal curvature in all directions is the same (for example, near a sphere or at the end of an ellipsoid of revolution), then all directions at a point are principal.
Surfaces with negative (left), zero (center) and positive (right) curvature.
Normal curvatures in the principal directions are called main curvatures; let's denote them κ 1 and κ 2. Size:
K= κ 1 κ 2called Gaussian curvature, full curvature or simply curvature surfaces. There is also the term curvature scalar, which implies the result of convolution of the curvature tensor; in this case, the curvature scalar is twice as large as the Gaussian curvature.
Gaussian curvature can be calculated via a metric, and is therefore an object of the intrinsic geometry of surfaces (note that the principal curvatures do not belong to the intrinsic geometry). You can classify surface points based on the sign of curvature (see figure). The curvature of the plane is zero. The curvature of a sphere of radius R is equal everywhere. There is also a surface of constant negative curvature - pseudosphere.
Geodesic lines, geodesic curvature
The curve on the surface is called geodetic line, or simply geodetic, if at all its points the main normal to the curve coincides with the normal to the surface. Example: on a plane, geodesics are straight lines and segments of straight lines, on a sphere - great circles and their segments.
Equivalent definition: for a geodesic line, the projection of its principal normal onto the osculating plane is the zero vector. If the curve is not geodesic, then the specified projection is nonzero; its length is called geodesic curvature k g curve on the surface. There is a relationship:
Where k- curvature of this curve, k n- the curvature of its normal section with the same tangent.
Geodesic lines refer to internal geometry. Let us list their main properties.
- Through a given surface point in a given direction there passes one and only one geodesic.
- On a sufficiently small area of the surface, two points can always be connected by a geodesic, and, moreover, only by one. Explanation: on a sphere, opposite poles are connected by an infinite number of meridians, and two close points can be connected not only by a segment of a large circle, but also by its addition to a complete circle, so that uniqueness is maintained only in the small.
- A geodesic is a shortest path. More strictly: on a small piece of surface the shortest path between given points lies along a geodesic.
Square
Another important attribute of the surface is its square, which is calculated by the formula:
In coordinates we get:
| explicit assignment | parametric specification | |
|---|---|---|
| area expression |  |
A surface is defined as a set of points whose coordinates satisfy a certain type of equation:
F (x , y , z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))If the function F (x , y , z) (\displaystyle F(x,\,y,\,z)) is continuous at some point and has continuous partial derivatives at it, at least one of which does not vanish, then in the neighborhood of this point the surface given by equation (1) will be the right surface.
In addition to the above implicit way of specifying, the surface can be defined obviously, if one of the variables, for example, z, can be expressed in terms of the others:
z = f (x , y) (1 ′) (\displaystyle z=f(x,y)\qquad (1"))More strictly simple surface is called the image of a homeomorphic mapping (that is, a one-to-one and mutually continuous mapping) of the interior of a unit square. This definition can be given an analytical expression.
Let a square be given on a plane with a rectangular coordinate system u and v, the coordinates of the internal points of which satisfy the inequalities 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").
Example simple surface is a hemisphere. The entire sphere is not simple surface. This necessitates further generalization of the concept of surface.
A subset of space, each point of which has a neighborhood that is simple surface, called the right surface .
Surface in differential geometry
Helicoid

Catenoid
The metric does not uniquely determine the shape of the surface. For example, the metrics of a helicoid and a catenoid, parameterized accordingly, coincide, that is, there is a correspondence between their regions that preserves all lengths (isometry). Properties that are preserved under isometric transformations are called internal geometry surfaces. The internal geometry does not depend on the position of the surface in space and does not change when it is bent without tension or compression (for example, when a cylinder is bent into a cone).
Metric coefficients E , F , G (\displaystyle E,\ F,\ G) determine not only the lengths of all curves, but also in general the results of all measurements inside the surface (angles, areas, curvature, etc.). Therefore, everything that depends only on the metric refers to internal geometry.
Normal and normal section

Normal vectors at surface points
One of the main characteristics of a surface is its normal- unit vector perpendicular to the tangent plane at a given point:
m = [ r u ′ , r v ′ ] | [ r u ′ , r v ′ ] | (\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (r"_(v)) ]|))).The sign of the normal depends on the choice of coordinates.
A section of a surface by a plane containing the surface normal at a given point forms a certain curve called normal section surfaces. The main normal for a normal section coincides with the normal to the surface (up to sign).
If the curve on the surface is not a normal section, then its main normal forms a certain angle with the normal of the surface θ (\displaystyle \theta ). Then the curvature k (\displaystyle k) curve related to curvature k n (\displaystyle k_(n)) normal section (with the same tangent) by Meunier's formula:
k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta )The coordinates of the normal unit vector for different methods of defining a surface are given in the table:
| Normal coordinates at a surface point | |
|---|---|
| implicit assignment | (∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(( \frac (\partial F)(\partial x));\,(\frac (\partial F)(\partial y));\,(\frac (\partial F)(\partial z))\right) )(\sqrt (\left((\frac (\partial F)(\partial x))\right)^(2)+\left((\frac (\partial F)(\partial y))\right) ^(2)+\left((\frac (\partial F)(\partial z))\right)^(2))))) |
| explicit assignment | (− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\partial f )(\partial x));\,-(\frac (\partial f)(\partial y));\,1\right))(\sqrt (\left((\frac (\partial f)(\ partial x))\right)^(2)+\left((\frac (\partial f)(\partial y))\right)^(2)+1)))) |
| parametric specification | (D (y, z) D (u, v) ; D (z, x) D (u, v) ; D (x, y) D (u, v)) (D (y, z) D (u , v)) 2 + (D (z , x) D (u , v)) 2 + (D (x , y) D (u , v)) 2 (\displaystyle (\frac (\left((\frac (D(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x ,y))(D(u,v)))\right))(\sqrt (\left((\frac (D(y,z))(D(u,v)))\right)^(2 )+\left((\frac (D(z,x))(D(u,v)))\right)^(2)+\left((\frac (D(x,y))(D( u,v)))\right)^(2))))) |
Here D (y , z) D (u , v) = | y u ′ y v ′ z u ′ z v ′ | , D (z , x) D (u , v) = | z u ′ z v ′ x u ′ x v ′ | , D (x, y) D (u, v) = | x u ′ x v ′ y u ′ y v ′ | (\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\begin(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatrix)),\quad (\frac (D(x,y))(D(u,v)))=(\ begin(vmatrix)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix))).
All derivatives are taken at the point (x 0 , y 0 , z 0) (\displaystyle (x_(0),y_(0),z_(0))).
Curvature
For different directions at a given point on the surface, different curvature of the normal section is obtained, which is called normal curvature; it is assigned a plus sign if the main normal of the curve goes in the same direction as the normal to the surface, or a minus sign if the directions of the normals are opposite.
Generally speaking, at every point on a surface there are two perpendicular directions e 1 (\displaystyle e_(1)) And e 2 (\displaystyle e_(2)), in which the normal curvature takes minimum and maximum values; these directions are called main. The exception is the case when the normal curvature in all directions is the same (for example, near a sphere or at the end of an ellipsoid of revolution), then all directions at a point are principal.
Surfaces with negative (left), zero (center) and positive (right) curvature.
Normal curvatures in the principal directions are called main curvatures; let's designate them κ 1 (\displaystyle \kappa _(1)) And κ 2 (\displaystyle \kappa _(2)). Size:
K = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))called Gaussian curvature, total curvature, or simply surface curvature. There is also the term curvature scalar, which implies the result of convolution of the curvature tensor; in this case, the curvature scalar is twice as large as the Gaussian curvature.
Gaussian curvature can be calculated via a metric, and is therefore an object of the intrinsic geometry of surfaces (note that the principal curvatures do not belong to the intrinsic geometry). You can classify surface points based on the sign of curvature (see figure). The curvature of the plane is zero. The curvature of a sphere of radius R is equal everywhere 1 R 2 (\displaystyle (\frac (1)(R^(2)))). There is also a surface of constant negative curvature -
Namely, about what you see in the title. Essentially, this is a “spatial analogue” tangent finding problems And normals to the graph of a function of one variable, and therefore no difficulties should arise.
Let's start with the basic questions: WHAT IS a tangent plane and WHAT IS a normal? Many people understand these concepts at the level of intuition. The simplest model that comes to mind is a ball on which lies a thin flat piece of cardboard. The cardboard is located as close as possible to the sphere and touches it at a single point. In addition, at the point of contact it is secured with a needle sticking straight up.
In theory, there is a rather ingenious definition of a tangent plane. Imagine a free surface and the point belonging to it. Obviously, a lot passes through the point spatial lines, which belong to this surface. Who has what associations? =) ...personally, I imagined an octopus. Let us assume that each such line has spatial tangent at point .
Definition 1: tangent plane to the surface at a point - this is plane, containing tangents to all curves that belong to a given surface and pass through the point.
Definition 2: normal to the surface at a point - this is straight, passing through a given point perpendicular to the tangent plane.
Simple and elegant. By the way, so that you don’t die of boredom from the simplicity of the material, a little later I will share with you one elegant secret that allows you to forget about cramming various definitions ONCE AND FOR ALL.
Let's get acquainted with the working formulas and solution algorithm using a specific example. In the vast majority of problems, it is necessary to construct both the tangent plane equation and the normal equation:
Example 1
Solution:if the surface is given by the equation (i.e. implicitly), then the equation of the tangent plane to a given surface at a point can be found using the following formula:
I pay special attention to unusual partial derivatives - their should not be confused With partial derivatives of an implicitly specified function (although the surface is specified implicitly). When finding these derivatives, one must be guided by rules for differentiating a function of three variables, that is, when differentiating with respect to any variable, the other two letters are considered constants:
Without leaving the cash register, we find the partial derivative at the point:
Likewise: 
This was the most unpleasant moment of the decision, in which an error, if not allowed, then constantly appears. However, there is an effective verification technique here, which I talked about in class. Directional derivative and gradient.
All the “ingredients” have been found and now it’s a matter of careful substitution with further simplifications: 
![]() – general equation the desired tangent plane.
– general equation the desired tangent plane.
I strongly recommend checking this stage of the solution as well. First you need to make sure that the coordinates of the tangent point really satisfy the found equation: ![]()
- true equality.
Now we “remove” the coefficients of the general equation of the plane and check them for coincidence or proportionality with the corresponding values. In this case they are proportional. As you remember from analytical geometry course, - This normal vector tangent plane, and he is also guide vector normal straight line. Let's compose canonical equations normals by point and direction vector: 
In principle, the denominators can be reduced by two, but there is no particular need for this
Answer:
It is not forbidden to designate the equations with some letters, but, again, why? Here it’s already extremely clear what’s what.
The following two examples are for you to solve on your own. A little “mathematical tongue twister”:
Example 2
Find the equations of the tangent plane and the normal to the surface at the point.
And a task that is interesting from a technical point of view:
Example 3
Write equations for the tangent plane and normal to the surface at a point
At the point.
There is every chance of not only getting confused, but also encountering difficulties when recording canonical equations of the line. And the normal equations, as you probably understand, are usually written in this form. Although, due to forgetfulness or ignorance of some nuances, the parametric form is more than acceptable.
Approximate examples of the final execution of solutions at the end of the lesson.
Is there a tangent plane at any point on the surface? In general, of course not. The classic example is conical surface ![]() and point - the tangents at this point directly form a conical surface, and, of course, do not lie in the same plane. It is easy to verify that something is wrong analytically: .
and point - the tangents at this point directly form a conical surface, and, of course, do not lie in the same plane. It is easy to verify that something is wrong analytically: .
Another source of problems is the fact non-existence any partial derivative at a point. However, this does not mean that at a given point there is no single tangent plane.
But it was, rather, popular science rather than practically significant information, and we return to pressing matters:
How to write equations for the tangent plane and normal at a point,
if the surface is specified by an explicit function?
Let's rewrite it implicitly:
And using the same principles we find partial derivatives: 
Thus, the tangent plane formula is transformed into the following equation:
And accordingly, the canonical normal equations:
![]()
As you might guess, ![]() - these are already “real” partial derivatives of a function of two variables at the point, which we used to denote by the letter “z” and were found 100500 times.
- these are already “real” partial derivatives of a function of two variables at the point, which we used to denote by the letter “z” and were found 100500 times.
Please note that in this article it is enough to remember the very first formula, from which, if necessary, it is easy to derive everything else (of course, having a basic level of training). This is exactly the approach that should be used when studying the exact sciences, i.e. from a minimum of information we must strive to “draw” a maximum of conclusions and consequences. “Consideration” and existing knowledge will help! This principle is also useful because it will most likely save you in a critical situation when you know very little.
Let’s work out the “modified” formulas with a couple of examples:
Example 4
Write equations for the tangent plane and normal to the surface ![]() at point .
at point .
There is a slight overlay here with the notations - now the letter denotes a point on the plane, but what can you do - such a popular letter...
Solution: let’s compose the equation of the desired tangent plane using the formula:
Let's calculate the value of the function at the point:
Let's calculate 1st order partial derivatives at this point: 
Thus:
carefully, don't rush: 
Let us write down the canonical equations of the normal at the point: 
Answer:
And a final example for your own solution:
Example 5
Write down equations for the tangent plane and the normal to the surface at the point.
Final - because I have explained virtually all the technical points and there is nothing special to add. Even the functions themselves proposed in this task are dull and monotonous - in practice you are almost guaranteed to come across a “polynomial”, and in this sense, Example No. 2 with an exponent looks like a “black sheep”. By the way, it is much more likely to encounter a surface defined by an equation, and this is another reason why the function was included in the article as number two.
And finally, the promised secret: so how to avoid cramming definitions? (I, of course, do not mean the situation when a student is feverishly cramming something before an exam)
The definition of any concept/phenomenon/object, first of all, gives an answer to the following question: WHAT IS IT? (who/such/such/are). Consciously When answering this question, you should try to reflect significant signs, definitely identifying a particular concept/phenomenon/object. Yes, at first it turns out to be somewhat tongue-tied, inaccurate and redundant (the teacher will correct you =)), but over time, quite decent scientific speech develops.
Practice on the most abstract objects, for example, answer the question: who is Cheburashka? It's not that simple ;-) Is this a “fairytale character with big ears, eyes and brown fur”? Far and very far from definition - you never know there are characters with such characteristics... But this is much closer to the definition: “Cheburashka is a character invented by the writer Eduard Uspensky in 1966, who ... (listing of the main distinguishing features)”. Notice how well it started
Let us have a surface defined by an equation of the form
Let us introduce the following definition.
Definition 1. A straight line is called tangent to the surface at some point if it is
tangent to any curve lying on the surface and passing through the point.
Since an infinite number of different curves lying on the surface pass through the point P, then, generally speaking, there will be an infinite number of tangents to the surface passing through this point.
Let us introduce the concept of singular and ordinary points of a surface
If at a point all three derivatives are equal to zero or at least one of these derivatives does not exist, then the point M is called a singular point of the surface. If at a point all three derivatives exist and are continuous, and at least one of them is different from zero, then the point M is called an ordinary point of the surface.
Now we can formulate the following theorem.
Theorem. All tangent lines to a given surface (1) at its ordinary point P lie in the same plane.

Proof. Let us consider a certain line L on the surface (Fig. 206) passing through a given point P of the surface. Let the curve under consideration be given by parametric equations
The tangent to the curve will be the tangent to the surface. The equations of this tangent have the form

If expressions (2) are substituted into equation (1), then this equation will turn into an identity with respect to t, since curve (2) lies on surface (1). Differentiating it by we get
![]()
The projections of this vector depend on - the coordinates of point P; note that since point P is ordinary, these projections at point P do not simultaneously vanish and therefore
![]()
tangent to a curve passing through point P and lying on the surface. The projections of this vector are calculated based on equations (2) at the value of the parameter t corresponding to point P.
Let us calculate the scalar product of vectors N and which is equal to the sum of the products of projections of the same name:
Based on equality (3), the expression on the right side is equal to zero, therefore,
From the last equality it follows that the vector LG and the tangent vector to curve (2) at point P are perpendicular. The above reasoning is valid for any curve (2) passing through point P and lying on the surface. Consequently, each tangent to the surface at point P is perpendicular to the same vector N and therefore all these tangents lie in the same plane perpendicular to the vector LG. The theorem has been proven.
Definition 2. The plane in which all tangent lines to the lines on the surface passing through its given point P are located is called the tangent plane to the surface at point P (Fig. 207).

Note that at singular points of the surface there may not be a tangent plane. At such points, the tangent lines to the surface may not lie in the same plane. For example, the vertex of a conical surface is a singular point.
The tangents to the conical surface at this point do not lie in the same plane (they themselves form a conical surface).
Let us write the equation of the tangent plane to the surface (1) at an ordinary point. Since this plane is perpendicular to vector (4), therefore, its equation has the form
If the equation of the surface is given in the form or the equation of the tangent plane in this case takes the form
Comment. If we put in formula (6), then this formula will take the form
![]()
its right-hand side is the complete differential of the function. Hence, . Thus, the total differential of a function of two variables at a point corresponding to the increments of the independent variables x and y is equal to the corresponding increment of the applicate of the tangent plane to the surface, which is the graph of this function.
Definition 3. A straight line drawn through a point on the surface (1) perpendicular to the tangent plane is called the normal to the surface (Fig. 207).