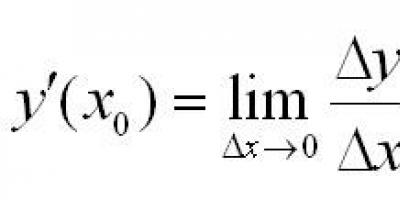Solving physical problems or examples in mathematics is completely impossible without knowledge of the derivative and methods for calculating it. The derivative is one of the most important concepts in mathematical analysis. We decided to devote today’s article to this fundamental topic. What is a derivative, what is its physical and geometric meaning, how to calculate the derivative of a function? All these questions can be combined into one: how to understand the derivative?
Geometric and physical meaning of derivative
Let there be a function f(x) , specified in a certain interval (a, b) . Points x and x0 belong to this interval. When x changes, the function itself changes. Changing the argument - the difference in its values x-x0 . This difference is written as delta x and is called argument increment. A change or increment of a function is the difference between the values of a function at two points. Definition of derivative:
The derivative of a function at a point is the limit of the ratio of the increment of the function at a given point to the increment of the argument when the latter tends to zero.
Otherwise it can be written like this:
What's the point of finding such a limit? And here's what it is:
the derivative of a function at a point is equal to the tangent of the angle between the OX axis and the tangent to the graph of the function at a given point.
Physical meaning of the derivative: the derivative of the path with respect to time is equal to the speed of rectilinear motion.
Indeed, since school days everyone knows that speed is a particular path x=f(t) and time t . Average speed over a certain period of time:
To find out the speed of movement at a moment in time t0 you need to calculate the limit:
Rule one: set a constant
The constant can be taken out of the derivative sign. Moreover, this must be done. When solving examples in mathematics, take it as a rule - If you can simplify an expression, be sure to simplify it .
Example. Let's calculate the derivative:
Rule two: derivative of the sum of functions
The derivative of the sum of two functions is equal to the sum of the derivatives of these functions. The same is true for the derivative of the difference of functions.
We will not give a proof of this theorem, but rather consider a practical example.
Find the derivative of the function:
Rule three: derivative of the product of functions
The derivative of the product of two differentiable functions is calculated by the formula:
Example: find the derivative of a function:
Solution: 
It is important to talk about calculating derivatives of complex functions here. The derivative of a complex function is equal to the product of the derivative of this function with respect to the intermediate argument and the derivative of the intermediate argument with respect to the independent variable.
In the above example we come across the expression:
In this case, the intermediate argument is 8x to the fifth power. In order to calculate the derivative of such an expression, we first calculate the derivative of the external function with respect to the intermediate argument, and then multiply by the derivative of the intermediate argument itself with respect to the independent variable.
Rule four: derivative of the quotient of two functions
Formula for determining the derivative of the quotient of two functions:
We tried to talk about derivatives for dummies from scratch. This topic is not as simple as it seems, so be warned: there are often pitfalls in the examples, so be careful when calculating derivatives.
With any questions on this and other topics, you can contact the student service. In a short time, we will help you solve the most difficult test and understand the tasks, even if you have never done derivative calculations before.
Prove formulas 3 and 5 yourself.
BASIC RULES OF DIFFERENTIATION
Using the general method of finding the derivative using the limit, one can obtain the simplest differentiation formulas. Let u=u(x),v=v(x)– two differentiable functions of a variable x.
Prove formulas 1 and 2 yourself.
Proof of Formula 3.
Let y = u(x) + v(x). For argument value x+Δ x we have y(x+Δ x)=u(x+Δ x) + v(x+Δ x).
Δ y=y(x+Δ x) – y(x) = u(x+Δ x) + v(x+Δ x) – u(x) – v(x) = Δ u +Δ v.
Hence,
Proof of formula 4.
Let y=u(x)·v(x). Then y(x+Δ x)=u(x+Δ x)· v(x+Δ x), That's why
Δ y=u(x+Δ x)· v(x+Δ x) – u(x)· v(x).
Note that since each of the functions u And v differentiable at the point x, then they are continuous at this point, which means u(x+Δ x)→u(x), v(x+Δ x)→v(x), at Δ x→0.
Therefore we can write
Based on this property, one can obtain a rule for differentiating the product of any number of functions.
Let, for example, y=u·v·w. Then,
y " = u "·( v w) + u·( v·w) " = u "· v·w + u·( v"·w+ v·w ") = u "· v·w + u· v"·w+ u·v·w ".
Proof of formula 5.
Let . Then
In the proof we used the fact that v(x+Δ x)→v(x) at Δ x→0.
Examples.
THEOREM ON THE DERIVATIVE OF COMPLEX FUNCTION
Let y = f(u), A u= u(x). We get the function y depending on the argument x: y = f(u(x)). The last function is called a function of a function or complex function.
Function definition domain y = f(u(x)) is either the entire domain of definition of the function u=u(x) or that part in which the values are determined u, not leaving the domain of definition of the function y= f(u).
The function-from-function operation can be performed not just once, but any number of times.
Let us establish a rule for differentiating a complex function.
Theorem. If the function u= u(x) has at some point x 0 derivative and takes the value at this point u 0 = u(x 0), and the function y=f(u) has at the point u 0 derivative y" u = f "(u 0), then a complex function y = f(u(x)) at the specified point x 0 also has a derivative, which is equal to y" x = f "(u 0)· u "(x 0), where instead of u the expression must be substituted u= u(x).
Thus, the derivative of a complex function is equal to the product of the derivative of a given function with respect to the intermediate argument u to the derivative of the intermediate argument with respect to x.
Proof. For a fixed value X 0 we will have u 0 =u(x 0), at 0 =f(u 0 ). For a new argument value x 0+Δ x:
Δ u= u(x 0 + Δ x) – u(x 0), Δ y=f(u 0+Δ u) – f(u 0).
Because u– differentiable at a point x 0, That u– is continuous at this point. Therefore, at Δ x→0 Δ u→0. Similarly for Δ u→0 Δ y→0.
By condition 
. From this relation, using the definition of the limit, we obtain (at Δ u→0)
where α→0 at Δ u→0, and, consequently, at Δ x→0.
Let us rewrite this equality as:
Δ y=y" uΔ u+α·Δ u.
The resulting equality is also valid for Δ u=0 for arbitrary α, since it turns into the identity 0=0. At Δ u=0 we will assume α=0. Let us divide all terms of the resulting equality by Δ x
.
By condition 
. Therefore, passing to the limit at Δ x→0, we get y" x = y"u·u" x. The theorem has been proven.
So, to differentiate a complex function y = f(u(x)), you need to take the derivative of the "external" function f, treating its argument simply as a variable, and multiply by the derivative of the "inner" function with respect to the independent variable.
If the function y=f(x) can be represented in the form y=f(u), u=u(v), v=v(x), then finding the derivative y " x is carried out by sequential application of the previous theorem.
According to the proven rule, we have y" x = y" u u"x. Applying the same theorem for u"x we get, i.e.
y" x = y" x u" v v" x = f"u( u)· u" v ( v)· v" x ( x).
Examples.
CONCEPT OF INVERSE FUNCTION
Let's start with an example. Consider the function y= x 3. We will consider the equality y= x 3 as an equation relative x. This is the equation for each value at defines a single value x: . Geometrically, this means that every straight line parallel to the axis Ox intersects the graph of a function y= x 3 only at one point. Therefore we can consider x as a function of y. A function is called the inverse of a function y= x 3.
Before moving on to the general case, we introduce definitions.
Function y = f(x) called increasing on a certain segment, if the larger value of the argument x from this segment corresponds to a larger value of the function, i.e. If x 2 >x 1, then f(x 2 ) > f(x 1 ).
The function is called similarly decreasing, if a smaller value of the argument corresponds to a larger value of the function, i.e. If X 2 < X 1, then f(x 2 ) > f(x 1 ).
So, let's be given an increasing or decreasing function y=f(x), defined on some interval [ a; b]. For definiteness, we will consider an increasing function (for a decreasing one everything is similar).
Consider two different values X 1 and X 2. Let y 1 =f(x 1 ), y 2 =f(x 2 ). From the definition of an increasing function it follows that if x 1 <x 2, then at 1 <at 2. Therefore, two different values X 1 and X 2 corresponds to two different function values at 1 and at 2. The opposite is also true, i.e. If at 1 <at 2, then from the definition of an increasing function it follows that x 1 <x 2. Those. again two different values at 1 and at 2 corresponds to two different values x 1 and x 2. Thus, between the values x and their corresponding values y a one-to-one correspondence is established, i.e. the equation y=f(x) for each y(taken from the range of the function y=f(x)) defines a single value x, and we can say that x there is some argument function y: x= g(y).
This function is called reverse for function y=f(x). Obviously, the function y=f(x) is the inverse of the function x=g(y).
Note that the inverse function x=g(y) found by solving the equation y=f(x) relatively X.
Example. Let the function be given y= e x . This function increases at –∞< x <+∞. Она имеет обратную функцию x= log y. Domain of inverse function 0< y < + ∞.
Let's make a few comments.
Note 1. If an increasing (or decreasing) function y=f(x) is continuous on the interval [ a; b], and f(a)=c, f(b)=d, then the inverse function is defined and continuous on the interval [ c; d].
Note 2. If the function y=f(x) is neither increasing nor decreasing on a certain interval, then it can have several inverse functions.
Example. Function y=x2 defined at –∞<x<+∞. Она не является ни возрастающей, ни убывающей и не имеет обратной функции. Однако, если мы рассмотриминтервал 0≤x<+∞, то здесь функция является возрастающей и обратной для нее будет . На интервале – ∞ <x≤ 0 function – decreases and its inverse.
Note 3. If the functions y=f(x) And x=g(y) are mutually inverse, then they express the same relationship between variables x And y. Therefore, the graph of both is the same curve. But if we denote the argument of the inverse function again by x, and the function through y and plot them in the same coordinate system, we will get two different graphs. It is easy to notice that the graphs will be symmetrical with respect to the bisector of the 1st coordinate angle.
THEOREM ON THE DERIVATIVE INVERSE FUNCTION
Let us prove a theorem that allows us to find the derivative of the function y=f(x), knowing the derivative of the inverse function.
Theorem. If for the function y=f(x) there is an inverse function x=g(y), which at some point at 0 has a derivative g "(v 0), nonzero, then at the corresponding point x 0=g(x 0) function y=f(x) has a derivative f "(x 0), equal to , i.e. the formula is correct.
Proof. Because x=g(y) differentiable at the point y 0, That x=g(y) is continuous at this point, so the function y=f(x) continuous at a point x 0=g(y 0). Therefore, at Δ x→0 Δ y→0.
Let's show that 
.
Let . Then, by the property of the limit 
. Let us pass in this equality to the limit at Δ y→0. Then Δ x→0 and α(Δx)→0, i.e. .
Hence,
,
Q.E.D.
This formula can be written in the form .
Let's look at the application of this theorem using examples.
When deriving the very first formula of the table, we will proceed from the definition of the derivative function at a point. Let's take where x– any real number, that is, x– any number from the domain of definition of the function. Let us write down the limit of the ratio of the increment of the function to the increment of the argument at : 
It should be noted that under the limit sign the expression is obtained, which is not the uncertainty of zero divided by zero, since the numerator does not contain an infinitesimal value, but precisely zero. In other words, the increment of a constant function is always zero.
Thus, derivative of a constant functionis equal to zero throughout the entire domain of definition.
Derivative of a power function.
The formula for the derivative of a power function has the form 
, where the exponent p– any real number.
Let us first prove the formula for the natural exponent, that is, for p = 1, 2, 3, …
We will use the definition of derivative. Let us write down the limit of the ratio of the increment of a power function to the increment of the argument: 
To simplify the expression in the numerator, we turn to the Newton binomial formula: 
Hence, 
This proves the formula for the derivative of a power function for a natural exponent.
Derivative of an exponential function.
We present the derivation of the derivative formula based on the definition:
We have arrived at uncertainty. To expand it, we introduce a new variable, and at . Then . In the last transition, we used the formula for transitioning to a new logarithmic base.
Let's substitute into the original limit: 
If we recall the second remarkable limit, we arrive at the formula for the derivative of the exponential function: 
Derivative of a logarithmic function.
Let us prove the formula for the derivative of a logarithmic function for all x from the domain of definition and all valid values of the base a logarithm By definition of derivative we have: 
As you noticed, during the proof the transformations were carried out using the properties of the logarithm. Equality 
is true due to the second remarkable limit.
Derivatives of trigonometric functions.
To derive formulas for derivatives of trigonometric functions, we will have to recall some trigonometry formulas, as well as the first remarkable limit.
By definition of the derivative for the sine function we have 
.
Let's use the difference of sines formula: 
It remains to turn to the first remarkable limit: 
Thus, the derivative of the function sin x There is cos x.
The formula for the derivative of the cosine is proved in exactly the same way. 
Therefore, the derivative of the function cos x There is –sin x.
We will derive formulas for the table of derivatives for tangent and cotangent using proven rules of differentiation (derivative of a fraction). 
Derivatives of hyperbolic functions.
The rules of differentiation and the formula for the derivative of the exponential function from the table of derivatives allow us to derive formulas for the derivatives of the hyperbolic sine, cosine, tangent and cotangent. 
Derivative of the inverse function.
To avoid confusion during presentation, let's denote in subscript the argument of the function by which differentiation is performed, that is, it is the derivative of the function f(x) By x.
Now let's formulate rule for finding the derivative of an inverse function.
Let the functions y = f(x) And x = g(y) mutually inverse, defined on the intervals and respectively. If at a point there is a finite non-zero derivative of the function f(x), then at the point there is a finite derivative of the inverse function g(y), and 
. In another post 
.
This rule can be reformulated for any x from the interval , then we get 
.
Let's check the validity of these formulas.
Let's find the inverse function for the natural logarithm 
(Here y is a function, and x- argument). Having resolved this equation for x, we get (here x is a function, and y– her argument). That is, 
and mutually inverse functions.
From the table of derivatives we see that 
And 
.
Let’s make sure that the formulas for finding the derivatives of the inverse function lead us to the same results: 
As you can see, we got the same results as in the derivatives table.
Now we have the knowledge to prove formulas for the derivatives of inverse trigonometric functions.
Let's start with the derivative of the arcsine.
. Then, using the formula for the derivative of the inverse function, we get
All that remains is to carry out the transformations.
Since the arcsine range is the interval 
, That 
(see the section on basic elementary functions, their properties and graphs). Therefore, we are not considering it.
Hence, 
. The domain of definition of the arcsine derivative is the interval (-1;
1)
.
For the arc cosine, everything is done in exactly the same way: 
Let's find the derivative of the arctangent.
For the inverse function is 
.
Let's express the arctangent in terms of arccosine to simplify the resulting expression.
Let arctgx = z, Then 
Hence, 
The derivative of the arc cotangent is found in a similar way: 
Very easy to remember.
Well, let’s not go far, let’s immediately consider the inverse function. Which function is the inverse of the exponential function? Logarithm:
In our case, the base is the number:
Such a logarithm (that is, a logarithm with a base) is called “natural”, and we use a special notation for it: we write instead.
What is it equal to? Of course, .
The derivative of the natural logarithm is also very simple:
Examples:
- Find the derivative of the function.
- What is the derivative of the function?
Answers: The exponential and natural logarithm are uniquely simple functions from a derivative perspective. Exponential and logarithmic functions with any other base will have a different derivative, which we will analyze later, after we go through the rules of differentiation.
Rules of differentiation
Rules of what? Again a new term, again?!...
Differentiation is the process of finding the derivative.
That's all. What else can you call this process in one word? Not derivative... Mathematicians call the differential the same increment of a function at. This term comes from the Latin differentia - difference. Here.
When deriving all these rules, we will use two functions, for example, and. We will also need formulas for their increments:
There are 5 rules in total.
The constant is taken out of the derivative sign.
If - some constant number (constant), then.
Obviously, this rule also works for the difference: .
Let's prove it. Let it be, or simpler.
Examples.
Find the derivatives of the functions:
- at a point;
- at a point;
- at a point;
- at the point.
Solutions:
- (the derivative is the same at all points, since it is a linear function, remember?);
Derivative of the product
Everything is similar here: let’s introduce a new function and find its increment:
Derivative:
Examples:
- Find the derivatives of the functions and;
- Find the derivative of the function at a point.
Solutions:
Derivative of an exponential function
Now your knowledge is enough to learn how to find the derivative of any exponential function, and not just exponents (have you forgotten what that is yet?).
So, where is some number.
We already know the derivative of the function, so let's try to bring our function to a new base:
To do this, we will use a simple rule: . Then:
Well, it worked. Now try to find the derivative, and don't forget that this function is complex.
Happened?
Here, check yourself:
The formula turned out to be very similar to the derivative of an exponent: as it was, it remains the same, only a factor appeared, which is just a number, but not a variable.
Examples:
Find the derivatives of the functions:
Answers:
This is just a number that cannot be calculated without a calculator, that is, it cannot be written down in a simpler form. Therefore, we leave it in this form in the answer.
Note that here is the quotient of two functions, so we apply the corresponding differentiation rule:
In this example, the product of two functions:
Derivative of a logarithmic function
It’s similar here: you already know the derivative of the natural logarithm:
Therefore, to find an arbitrary logarithm with a different base, for example:
We need to reduce this logarithm to the base. How do you change the base of a logarithm? I hope you remember this formula:
Only now we will write instead:
The denominator is simply a constant (a constant number, without a variable). The derivative is obtained very simply:
Derivatives of exponential and logarithmic functions are almost never found in the Unified State Examination, but it will not be superfluous to know them.
Derivative of a complex function.
What is a "complex function"? No, this is not a logarithm, and not an arctangent. These functions can be difficult to understand (although if you find the logarithm difficult, read the topic “Logarithms” and you will be fine), but from a mathematical point of view, the word “complex” does not mean “difficult”.
Imagine a small conveyor belt: two people are sitting and doing some actions with some objects. For example, the first one wraps a chocolate bar in a wrapper, and the second one ties it with a ribbon. The result is a composite object: a chocolate bar wrapped and tied with a ribbon. To eat a chocolate bar, you need to do the reverse steps in reverse order.
Let's create a similar mathematical pipeline: first we will find the cosine of a number, and then square the resulting number. So, we are given a number (chocolate), I find its cosine (wrapper), and then you square what I got (tie it with a ribbon). What happened? Function. This is an example of a complex function: when, to find its value, we perform the first action directly with the variable, and then a second action with what resulted from the first.
In other words, a complex function is a function whose argument is another function: .
For our example, .
We can easily do the same steps in reverse order: first you square it, and I then look for the cosine of the resulting number: . It’s easy to guess that the result will almost always be different. An important feature of complex functions: when the order of actions changes, the function changes.
Second example: (same thing). .
The action we do last will be called "external" function, and the action performed first - accordingly "internal" function(these are informal names, I use them only to explain the material in simple language).
Try to determine for yourself which function is external and which internal:
Answers: Separating inner and outer functions is very similar to changing variables: for example, in a function
- What action will we perform first? First, let's calculate the sine, and only then cube it. This means that it is an internal function, but an external one.
And the original function is their composition: . - Internal: ; external: .
Examination: . - Internal: ; external: .
Examination: . - Internal: ; external: .
Examination: . - Internal: ; external: .
Examination: .
We change variables and get a function.
Well, now we will extract our chocolate bar and look for the derivative. The procedure is always reversed: first we look for the derivative of the outer function, then we multiply the result by the derivative of the inner function. In relation to the original example, it looks like this:
Another example:
So, let's finally formulate the official rule:
Algorithm for finding the derivative of a complex function:
It seems simple, right?
Let's check with examples:
Solutions:
1) Internal: ;
External: ;
2) Internal: ;
(Just don’t try to cut it by now! Nothing comes out from under the cosine, remember?)
3) Internal: ;
External: ;
It is immediately clear that this is a three-level complex function: after all, this is already a complex function in itself, and we also extract the root from it, that is, we perform the third action (put the chocolate in a wrapper and with a ribbon in the briefcase). But there is no reason to be afraid: we will still “unpack” this function in the same order as usual: from the end.
That is, first we differentiate the root, then the cosine, and only then the expression in brackets. And then we multiply it all.
In such cases, it is convenient to number the actions. That is, let's imagine what we know. In what order will we perform actions to calculate the value of this expression? Let's look at an example:
The later the action is performed, the more “external” the corresponding function will be. The sequence of actions is the same as before:
Here the nesting is generally 4-level. Let's determine the course of action.
1. Radical expression. .
2. Root. .
3. Sine. .
4. Square. .
5. Putting it all together:
DERIVATIVE. BRIEFLY ABOUT THE MAIN THINGS
Derivative of a function- the ratio of the increment of the function to the increment of the argument for an infinitesimal increment of the argument:
Basic derivatives:
Rules of differentiation:
The constant is taken out of the derivative sign:
Derivative of the sum:
Derivative of the product:
Derivative of the quotient:
Derivative of a complex function:
Algorithm for finding the derivative of a complex function:
- We define the “internal” function and find its derivative.
- We define the “external” function and find its derivative.
- We multiply the results of the first and second points.
Calculation of the derivative is often found in Unified State Examination tasks. This page contains a list of formulas for finding derivatives.
Rules of differentiation
- (k⋅ f(x))′=k⋅ f ′(x).
- (f(x)+g(x))′=f′(x)+g′(x).
- (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
- Derivative of a complex function. If y=F(u), and u=u(x), then the function y=f(x)=F(u(x)) is called a complex function of x. Equal to y′(x)=Fu′⋅ ux′.
- Derivative of an implicit function. The function y=f(x) is called an implicit function defined by the relation F(x,y)=0 if F(x,f(x))≡0.
- Derivative of the inverse function. If g(f(x))=x, then the function g(x) is called the inverse function of the function y=f(x).
- Derivative of a parametrically defined function. Let x and y be specified as functions of the variable t: x=x(t), y=y(t). They say that y=y(x) is a parametrically defined function on the interval x∈ (a;b), if on this interval the equation x=x(t) can be expressed as t=t(x) and the function y=y( t(x))=y(x).
- Derivative of a power-exponential function. Found by taking logarithms to the base of the natural logarithm.
