Let us establish a connection between the displacement of an oscillating particle of the medium (point) from the equilibrium position and the time counted from the moment of the beginning of oscillation of the source, which is located at a distance X from “our” particle at the origin.
Let the vibrations of the source S harmonic, i.e. are described by the equation ξ (t)= A sin ωt. Over time, all particles of the medium will also perform sinusoidal oscillations with the same frequency and amplitude, but with different phases. A harmonic traveling wave will arise in the medium.
Particle of the medium located on the axis OH on distance X from source S(Fig. 1.2), will begin to oscillate later than the source, for the time required for the wave propagating from the source at a speed V, covered the distance X to a particle. Obviously, if the source fluctuates over time t, then the particle of the medium oscillates only during time ( t – t) , where t is the time of propagation of oscillations from the source to the particle.
Then the vibration equation for this particle will be
ξ (x,t)=A sinω( t-τ),
but t =x/V, Where V– modulus of wave propagation speed. Then
ξ (x,t)=A sinω( t-x/V)
– wave equation.
Taking into account the fact that and , the equation can be given the form
ξ (x,t)=A sin2 ( t/T-x/λ) = A sin2(ν t -x/λ) = A sin (ω t -2πx/λ) = A sin (ω t-kx),(1.1)
Where k = 2p/ l– wave number. Here (1.1) is the equation of a plane harmonic monochromatic wave (Fig. 1.3), propagating in the direction of the axis OH. The wave graph is superficially similar to the harmonic oscillation graph, but in essence they are different.
 |
Oscillation graph - the dependence of the displacement of a given particle on time. The wave graph is the displacement of all particles of the medium at a given moment in time at the entire distance from the source of oscillations to the wave front. A wave chart is like a snapshot of a wave.
The equation of a traveling wave propagating in an arbitrary direction has the form:
ξ (x,y,z,t) = A sin = A sin( ωt – k x x – k y y – k z z), (1.2)
Where ξ – instantaneous displacement of an oscillating element of the medium (point) with coordinates x, y, z; A– displacement amplitude; ω – circular frequency of oscillations;
– wave vector equal to ( – unit vector indicating the direction of wave propagation); 
; - orts;
λ – wavelength (Fig. 1.3), i.e. the distance over which the wave propagates in a time equal to the period of oscillation of the particles of the medium; – radius vector drawn to the point under consideration, 
;
– phase of the wave, where 
.
Here are the angles formed by the wave vector with the corresponding coordinate axes.
If a wave propagates in a medium that does not absorb energy, then the amplitude of the wave does not change, i.e. A= const .
The speed of propagation of wave motion is the speed of propagation of the phase of the wave (phase speed). In a homogeneous medium, the wave speed is constant. If the phase velocity of a wave in a medium depends on frequency, then this phenomenon is called wave dispersion, and the medium is called a dispersive medium.
When moving from one medium to another, the speed of wave propagation may change, since the elastic properties of the medium change, but the frequency of oscillations, as experience shows, remains unchanged. It means that When moving from one medium to another, the wavelength l will change.
If we excite oscillations at any point in the medium, then the oscillations will be transmitted to all points surrounding it, i.e. a set of particles contained in a certain volume will oscillate. Propagating from the source of vibrations, the wave process covers more and more new parts of space. The geometric location of the points to which the oscillations reach at a certain time t is called the wave front.
Thus, the wave front is the surface that separates the part of space already involved in the wave process from the region in which oscillations have not yet arisen. The geometric location of points oscillating in the same phase is called a wave surface. Wave surfaces can be of various shapes. The simplest of them have the shape of a sphere or plane. Waves having such surfaces are called spherical or plane, respectively.
Often, when solving problems of wave propagation, it is necessary to construct a wave front for a certain moment in time along the wave front specified for the initial moment in time. This can be done using Huygens principle , the essence of which is as follows.
Let the wave front moving in a homogeneous medium occupy position 1 at a given moment in time (Fig. 1.4). It is required to find its position after a period of time D t.
 |
According to Huygens' principle, every point in the medium to which the wave has reached becomes a source of secondary waves (first position of Huygens' principle).
This means that a spherical wave begins to propagate from it, as from the center. To construct secondary waves, around each point of the initial front we describe spheres of radius D x = V D t, Where V – wave speed . In Fig. 1.4 shows such spheres. Here the circles are sections of spherical surfaces by the drawing plane.
Secondary waves are mutually canceled out in all directions except the directions of the initial front(the second position of Huygens’ principle), that is, the oscillations are preserved only on the outer envelope of the secondary waves. Having constructed this envelope, we obtain the initial position of wave front 2 (dashed line). Wavefront positions 1 and 2
− in our case, planes.
Huygens' principle is also applicable to inhomogeneous media. In this case the values V, and, therefore, D X are not the same in different directions.
Since the passage of a wave is accompanied by vibrations of the particles of the medium, the energy of vibrations moves in space along with the wave.
Running waves are called waves that transfer energy and momentum in space. Energy transfer by waves is characterized energy flux density vector. The direction of this vector coincides with the direction of energy transfer, and its magnitude is called wave intensity (or energy flux density) and represents the ratio of energy W, carried by a wave through an area S┴ , perpendicular to the beam, to the duration of the transfer time ∆t and area size:
I = W/(∆t∙S ┴),
from where numerically I=W, If ∆t=1 and S┴ =1. Intensity unit: watt per meter squared (W/m 2 ).
We obtain an expression for the wave intensity. At concentration n 0 particles of the medium, each of which has mass m, bulk density w 0 energy consists of the kinetic energy of the movement of particles of the medium and potential energy, which is the energy of the deformed volume. Volumetric energy density is determined by the expression:
w 0 = n 0 mw 2 A 2 / 2= rw 2 A 2 / 2,
Where r =n 0 m. A detailed derivation of the expression for the volumetric energy density of elastic waves is given in the textbook. Obviously for 1 With through the platform at 1 m 2 the energy contained in the volume of a rectangular parallelepiped with base 1 is transferred m 2 and height numerically equal to speed V(Fig. 1.5) , hence the wave intensity
I = w 0 V = rVw 2 A 2 / 2. (1.3)
Thus, the intensity of the wave is proportional to the density of the medium, speed, square of the circular frequency and square of the amplitude of the wave
.
The vector, whose modulus is equal to the wave intensity, and whose direction coincides with the direction of wave propagation (and energy transfer), is determined by the expression.
PLATE WAVE
PLATE WAVE
A wave whose direction of propagation is the same at all points in space. The simplest example is a homogeneous monochromatic. undamped P.v.:
u(z, t)=Aeiwt±ikz, (1)
where A is the amplitude, j= wt±kz - , w=2p/T - circular frequency, T - oscillation period, k - . Constant phase surfaces (phase fronts) j=const P.v. are planes.
In the absence of dispersion, when vph and vgr are identical and constant (vgr = vph = v), there are stationary (i.e., moving as a whole) running linear motions, which allow a general representation of the form:
u(z, t)=f(z±vt), (2)
where f is an arbitrary function. In nonlinear media with dispersion, stationary running PVs are also possible. type (2), but their shape is no longer arbitrary, but depends both on the parameters of the system and on the nature of the movement. In absorbing (dissipative) media P. v. decrease their amplitude as they spread; with linear damping, this can be taken into account by replacing k in (1) with the complex wave number kd ± ikм, where km is the coefficient. attenuation of P. v.
A homogeneous PV that occupies the entire infinite is an idealization, but any wave concentrated in a finite region (for example, directed by transmission lines or waveguides) can be represented as a superposition of PV. with one space or another. spectrum k. In this case, the wave may still have a flat phase front, but non-uniform amplitude. Such P. v. called plane inhomogeneous waves. Some areas are spherical. and cylindrical waves that are small compared to the radius of curvature of the phase front behave approximately like a phase wave.
Physical encyclopedic dictionary. - M.: Soviet Encyclopedia. . 1983 .
PLATE WAVE
- wave, the direction of propagation is the same at all points in space.
Where A - amplitude, - phase, - circular frequency, T - period of oscillation k- wave number. = const P.v. are planes.
In the absence of dispersion, when the phase velocity v f and group v gr are identical and constant ( v gr = v f = v) there are stationary (i.e., moving as a whole) running P. c., which can be represented in general form
Where f- arbitrary function. In nonlinear media with dispersion, stationary running PVs are also possible. type (2), but their shape is no longer arbitrary, but depends both on the parameters of the system and on the nature of the wave motion. In absorbing (dissipative) media, P. k on the complex wave number k d ik m, where k m - coefficient attenuation of P. v. A homogeneous wave field that occupies the entire infinity is an idealization, but any wave field concentrated in a finite region (for example, directed transmission lines or waveguides), can be represented as a superposition P. V. with one or another spatial spectrum k. In this case, the wave may still have a flat phase front, with a non-uniform amplitude distribution. Such P. v. called plane inhomogeneous waves. Dept. areasspherical or cylindrical waves that are small compared to the radius of curvature of the phase front behave approximately like PT.
Lit. see under Art. Waves.
M. A. Miller, L. A. Ostrovsky.
Physical encyclopedia. In 5 volumes. - M.: Soviet Encyclopedia. Editor-in-chief A. M. Prokhorov. 1988 .
The wave equation is an expression that gives the displacement of an oscillating particle as a function of its coordinates x, y, z and time t:
(meaning the coordinates of the equilibrium position of the particle). This function must be periodic both with respect to time t and with respect to the coordinates x, y, z. Periodicity in time follows from the fact that it describes the oscillations of a particle with coordinates x, y, z. Periodicity in coordinates follows from the fact that points separated from each other by a distance K vibrate in the same way.
Let us find the form of the function in the case of a plane wave, assuming that the oscillations are harmonic in nature. To simplify, let us direct the coordinate axes so that the axis coincides with the direction of wave propagation. Then the wave surfaces will be perpendicular to the axis and, since all points of the wave surface vibrate equally, the displacement will depend only on Let the oscillations of points lying in the plane (Fig. 94.1) have the form
Let us find the type of oscillation of points in the plane corresponding to an arbitrary value of x. In order to travel from the plane x = 0 to this plane, the wave requires time - the speed of propagation of the wave).
Consequently, the oscillations of particles lying in the x-plane will lag in time from the oscillations of particles in the plane, i.e., they will have the form
So, the equation of a plane wave (both longitudinal and transverse) propagating in the x-axis direction is as follows:
The quantity a represents the amplitude of the wave. The initial phase of the wave a is determined by the choice of origins. When considering a single wave, the origins of time and coordinates are usually chosen so that a is equal to zero. When considering several waves together, it is usually not possible to ensure that the initial phases for all of them are equal to zero.
Let us fix any value of the phase in equation (94.2) by putting
(94.3)
This expression defines the relationship between time t and the place x at which the phase has a fixed value. The resulting value gives the speed at which a given phase value moves. Differentiating expression (94.3), we obtain
Thus, the speed of wave propagation v in equation (94.2) is the speed of phase movement, and therefore it is called the phase speed.
According to (94.4). Consequently, equation (94.2) describes a wave propagating in the direction of increasing x. A wave propagating in the opposite direction is described by the equation
Indeed, by equating the phase of the wave (94.5) to a constant and differentiating the resulting equality, we arrive at the relation
from which it follows that wave (94.5) propagates in the direction of decreasing x.
The plane wave equation can be given a form that is symmetrical with respect to x and t. To do this, we introduce the quantity
which is called the wave number. Having reduced the numerator and denominator of expression (94.6) to frequency v, we can represent the wave number in the form
(see formula (93.2)). Opening the parentheses in (94.2) and taking into account (94.7), we arrive at the following equation for a plane wave propagating along the x axis:
The equation of a wave propagating in the direction of decreasing x differs from (94.8) only in the sign of the term
When deriving formula (94.8), we assumed that the amplitude of oscillations does not depend on x. For a plane wave, this is observed in the case when the wave energy is not absorbed by the medium. When propagating in an energy-absorbing medium, the intensity of the wave gradually decreases with distance from the source of oscillations - wave attenuation is observed. Experience shows that in a homogeneous medium such attenuation occurs according to an exponential law: with a decrease in time of the amplitude of the damped oscillations; see formula (58.7) of the 1st volume). Accordingly, the plane wave equation has the following form:
Amplitude at points of the plane
Now let's find the equation of a spherical wave. Every real source of waves has some extent. However, if we limit ourselves to considering waves at distances from the source that significantly exceed its dimensions, then the source can be considered a point source. In an isotropic and homogeneous medium, the wave generated by a point source will be spherical. Let us assume that the phase of the source’s oscillations is equal. Then the points lying on the wave surface of radius will oscillate with the phase
Wave equation is an equation expressing the dependence of the displacement of an oscillating particle participating in a wave process on the coordinate of its equilibrium position and time:
This function must be periodic both with respect to time and with respect to coordinates. In addition, points located at a distance l from each other, oscillate in the same way.
Let's find the type of function x in the case of a plane wave.
Let us consider a plane harmonic wave propagating along the positive direction of the axis in a medium that does not absorb energy. In this case, the wave surfaces will be perpendicular to the axis. All quantities characterizing the oscillatory motion of particles of the medium depend only on time and coordinates. The offset will depend only on and: 
. Let the oscillation of a point with a coordinate (the source of oscillation) be given by the function. Task: find the type of vibration of points in the plane corresponding to an arbitrary value. In order to travel from a plane to this plane, a wave requires time. Consequently, the oscillations of particles lying in the plane will lag in phase by a time from the oscillations of particles in the plane. Then the equation of particle oscillations in the plane will have the form:
As a result, we obtained the equation of a plane wave propagating in the increasing direction:
. (3)
In this equation, is the amplitude of the wave; – cyclic frequency; – initial phase, which is determined by the choice of the reference point and ; 
– plane wave phase.
Let the wave phase be a constant value (we fix the phase value in the wave equation):
Let's reduce this expression by and differentiate. As a result we get:
or .
Thus, the speed of propagation of a wave in the plane wave equation is nothing more than the speed of propagation of a fixed phase of the wave. This speed is called phase velocity .
For a sine wave, the speed of energy transfer is equal to the phase speed. But a sine wave does not carry any information, and any signal is a modulated wave, i.e. not sinusoidal (not harmonic). When solving some problems, it turns out that the phase speed is greater than the speed of light. There is no paradox here, because... the speed of phase movement is not the speed of transmission (propagation) of energy. Energy and mass cannot move at a speed greater than the speed of light c .
Usually the plane wave equation is given a relatively symmetrical form. To do this, enter the value 
, which is called wave number
. Let us transform the expression for the wave number. Let's write it in the form 
(
). Let's substitute this expression into the plane wave equation:
Finally we get
This is the equation of a plane wave propagating in the increasing direction. The opposite direction of wave propagation will be characterized by an equation in which the sign in front of the term will change.
It is convenient to write the plane wave equation in the following form.
Usually a sign Re are omitted, implying that only the real part of the corresponding expression is taken. In addition, a complex number is introduced.
This number is called the complex amplitude. The modulus of this number gives the amplitude, and the argument gives the initial phase of the wave.
Thus, the equation of a plane continuous wave can be represented in the following form.
Everything discussed above related to a medium where there was no wave attenuation. In the case of wave attenuation, in accordance with Bouguer's law (Pierre Bouguer, French scientist (1698 - 1758)), the amplitude of the wave will decrease as it propagates. Then the plane wave equation will have the following form.
a– wave attenuation coefficient. A 0 – amplitude of oscillations at a point with coordinates . This is the reciprocal of the distance at which the wave amplitude decreases by e once.
Let's find the equation of a spherical wave. We will consider the source of oscillations to be point-like. This is possible if we limit ourselves to considering the wave at a distance much greater than the size of the source. A wave from such a source in an isotropic and homogeneous medium will be spherical . Points lying on the wave surface of radius will oscillate with phase
The amplitude of oscillations in this case, even if the wave energy is not absorbed by the medium, will not remain constant. It decreases with distance from the source according to the law. Therefore, the spherical wave equation has the form:
or
Due to the assumptions made, the equation is valid only for , significantly exceeding the size of the wave source. Equation (6) is not applicable for small values, because the amplitude would tend to infinity, and this is absurd.
In the presence of attenuation in the medium, the equation of a spherical wave will be written as follows.
Group speed
A strictly monochromatic wave is an infinite sequence of “humps” and “valleys” in time and space.
The phase speed of this wave or 
(2)
It is impossible to transmit a signal using such a wave, because at any point in the wave all the “humps” are the same. The signal must be different. To be a sign (mark) on the wave. But then the wave will no longer be harmonic, and will not be described by equation (1). A signal (pulse) can be represented according to Fourier’s theorem as a superposition of harmonic waves with frequencies contained in a certain interval Dw . Superposition of waves that differ little from each other in frequency,
 |
called wave packet or group of waves .
The expression for a group of waves can be written as follows.
(3)
Icon w emphasizes that these quantities depend on frequency.
This wave packet can be a sum of waves with slightly different frequencies. Where the phases of the waves coincide, an increase in amplitude is observed, and where the phases are opposite, a damping of the amplitude is observed (the result of interference). This picture is shown in the figure. In order for a superposition of waves to be considered a group of waves, the following condition must be met: Dw<< w 0 .
In a non-dispersive medium, all plane waves forming a wave packet propagate with the same phase velocity v . Dispersion is the dependence of the phase velocity of a sinusoidal wave in a medium on frequency. We will consider the phenomenon of dispersion later in the section “Wave Optics”. In the absence of dispersion, the speed of movement of the wave packet coincides with the phase speed v . In a dispersive medium, each wave disperses at its own speed. Therefore, the wave packet spreads out over time and its width increases.
If the dispersion is small, then the wave packet does not spread out too quickly. Therefore, a certain speed can be attributed to the movement of the entire package U
.
The speed at which the center of the wave packet (the point with the maximum amplitude) moves is called group velocity.
In a dispersive environment v¹U . Along with the movement of the wave packet itself, the “humps” inside the packet itself move. "Humps" move in space at speed v , and the package as a whole with speed U .
Let us consider in more detail the movement of a wave packet using the example of a superposition of two waves with the same amplitude and different frequencies w (different wavelengths l ).
Let's write down the equations of two waves. For simplicity, let us assume the initial phases j 0 = 0.
Here 
Let Dw<< w , respectively Dk<< k .
Let's add up the vibrations and carry out transformations using the trigonometric formula for the sum of cosines:
In the first cosine we will neglect Dwt And Dkx , which are much smaller than other quantities. Let's take into account that cos(–a) = cosa . We'll write it down finally.
(4)
The multiplier in square brackets changes with time and coordinates much more slowly than the second multiplier. Consequently, expression (4) can be considered as an equation of a plane wave with an amplitude described by the first factor. Graphically, the wave described by expression (4) is presented in the figure shown above.
The resulting amplitude is obtained as a result of the addition of waves, therefore, maxima and minima of the amplitude will be observed.
The maximum amplitude will be determined by the following condition.
(5)
m = 0, 1, 2…
xmax– coordinate of the maximum amplitude.
The cosine takes its maximum modulo value through p .
Each of these maxima can be considered as the center of the corresponding group of waves.
Resolving (5) relatively xmax we'll get it.
Since the phase speed is 
called group velocity. The maximum amplitude of the wave packet moves at this speed. In the limit, the expression for the group velocity will have the following form.
(6)
This expression is valid for the center of a group of an arbitrary number of waves.
It should be noted that when all terms of the expansion are accurately taken into account (for an arbitrary number of waves), the expression for the amplitude is obtained in such a way that it follows that the wave packet spreads out over time.
The expression for group velocity can be given a different form.
In the absence of variance 
The maximum intensity occurs at the center of the wave group. Therefore, the speed of energy transfer is equal to the group speed.
The concept of group velocity is applicable only under the condition that wave absorption in the medium is low. With significant wave attenuation, the concept of group velocity loses its meaning. This case is observed in the region of anomalous dispersion. We will consider this in the “Wave Optics” section.
As a manuscript
Physics
Lecture notes
(Part 5. Waves, wave optics)
For students direction 230400
"Information systems and technologies"
Electronic educational resource
Compiled by: Ph.D., Associate Professor V.V. Konovalenko
Protocol No. 1 dated 09/04/2013
Wave processes
Basic concepts and definitions
Let's consider some elastic medium - solid, liquid or gaseous. If vibrations of its particles are excited in any place of this medium, then due to the interaction between the particles, the vibrations will, transmitted from one particle of the medium to another, propagate through the medium at a certain speed. Process propagation of vibrations in space is called wave .
If particles in a medium oscillate in the direction of propagation of the wave, then it is called longitudinal
If particle oscillations occur in a plane perpendicular to the direction of propagation of the wave, then the wave is called transverse
. Transverse mechanical waves can only arise in a medium with a non-zero shear modulus. Therefore, they can spread in liquid and gaseous media only longitudinal waves
.
The difference between longitudinal and transverse waves is most clearly seen in the example of the propagation of vibrations in a spring - see figure.
To characterize transverse vibrations, it is necessary to set the position in space plane passing through the direction of oscillation and the direction of wave propagation - plane of polarization .
The region of space in which all particles of the medium vibrate is called wave field . The boundary between the wave field and the rest of the medium is called wave front . In other words, wave front - the geometric location of the points to which the oscillations have reached at a given point in time. In a homogeneous and isotropic medium, the direction of wave propagation is perpendicular to the wave front.
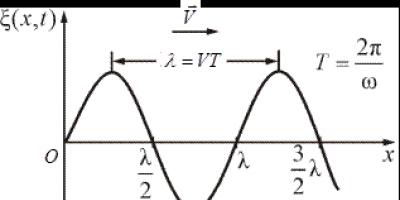
While a wave exists in the medium, the particles of the medium oscillate around their equilibrium positions. Let these oscillations be harmonic, and the period of these oscillations is T. Particles separated by a distance
along the direction of wave propagation, oscillate in the same way, i.e. at any given moment in time their displacements are the same. The distance is called wavelength . In other words, wavelength is the distance a wave travels in one period of oscillation .
The geometric location of points that oscillate in the same phase is called wave surface . A wave front is a special case of a wave surface. Wavelength – minimum the distance between two wave surfaces in which the points vibrate in the same way, or we can say that the phases of their oscillations differ by .
If the wave surfaces are planes, then the wave is called flat , and if by spheres, then spherical. A plane wave is excited in a continuous homogeneous and isotropic medium when an infinite plane oscillates. The excitation of a spherical surface can be represented as a result of radial pulsations of a spherical surface, and also as a result of the action point source, the dimensions of which can be neglected compared to the distance to the observation point. Since any real source has finite dimensions, at a sufficiently large distance from it the wave will be close to spherical. At the same time, the section of the wave surface of a spherical wave, as its size decreases, becomes arbitrarily close to the section of the wave surface of a plane wave.
Equation of a plane wave propagating
In any direction
We'll get it. Let the oscillations in a plane parallel to the wave surfaces and passing through the origin of coordinates have the form:
In a plane spaced from the origin by a distance l, the oscillations will lag in time by . Therefore, the equation of oscillations in this plane has the form:
From analytical geometry it is known that the distance from the origin to a certain plane is equal to the scalar product of the radius vector of a certain point on the plane and the unit vector normal to the plane: . The figure illustrates this situation for a two-dimensional case. Let's substitute the value l into equation (22.13):
(22.14)
A vector equal in magnitude to the wave number and directed normal to the wave surface is called wave vector . The plane wave equation can now be written as:
Function (22.15) gives the deviation from the equilibrium position of a point with a radius vector at the moment of time t. In order to represent the dependence on coordinates and time explicitly, it is necessary to take into account that
. (22.16)
Now the plane wave equation takes the form:
Often found useful represent the wave equation in exponential form . To do this, we use Euler's formula:
where , we write equation (22.15) in the form:
. (22.19)
Wave equation
The equation of any wave is a solution to a second order differential equation called wave . In order to establish the form of this equation, we find the second derivatives with respect to each of the arguments of the plane wave equation (22.17):
, (22.20)
, (22.21)
, (22.22)
Let's add the first three equations with derivatives with respect to coordinates:
. (22.24)
Let us express from equation (22.23): 
, and take into account that:
(22.25)
We present the sum of the second derivatives on the left side of (22.25) as the result of the action of the Laplace operator on , and in the final form we present wave equation as:
(22.26)
It is noteworthy that in the wave equation, the square root of the reciprocal of the coefficient of the time derivative gives the speed of wave propagation.
It can be shown that the wave equation (22.26) is satisfied by any function of the form:
And each of them is wave equation and describes a certain wave.
Elastic wave energy
Let us consider in a medium in which an elastic wave (22.10) propagates, an elementary volume small enough so that the deformation and velocity of the particles in it can be considered constant and equal:
Due to wave propagation in the medium, the volume has elastic deformation energy
(22.38)
In accordance with (22.35), the Young's modulus can be represented as . That's why:
. (22.39)
The volume under consideration also has kinetic energy:
. (22.40)
Total volume energy:
And the energy density:
, A 
(22.43)
Let's substitute these expressions into (22.42) and take into account that:
Thus, energy density is different at different points in space and changes over time according to the law of the square of sine.
The average value of the square of the sine is 1/2, which means average over time, the energy density value at each point in the medium , in which the wave propagates:
. (22.45)
Expression (22.45) is valid for all types of waves.
So, the medium in which the wave propagates has an additional supply of energy. Hence, the wave carries energy with it .
X.6 Dipole radiation
Oscillating electric dipole, i.e. a dipole, the electric moment of which changes periodically, for example, according to a harmonic law, is the simplest system emitting electromagnetic waves. One important example of an oscillating dipole is a system consisting of a negative charge that oscillates near a positive charge. This is exactly the situation that occurs when an electromagnetic wave acts on an atom of a substance, when, under the influence of the wave’s field, electrons oscillate in the vicinity of the atomic nucleus.
Let us assume that the dipole moment changes according to a harmonic law:
where is the radius vector of the negative charge, l- amplitude of oscillation, - unit vector directed along the dipole axis.
Let us limit ourselves to considering elementary dipole
, whose dimensions are small compared to the emitted wavelength and consider wave zone
dipoles, i.e. region of space for which the modulus of the radius vector of a point is . In the wave zone of a homogeneous and isotropic medium, the wave front will be spherical - Figure 22.4.
Electrodynamic calculation shows that the wave vector lies in a plane passing through the dipole axis and the radius vector of the point under consideration. Amplitudes and depend on distance r and the angle between and the axis of the dipole. In a vacuum
Since the Poynting vector is
, (22.33)
and it can be argued that the dipole radiates most strongly in the directions corresponding to , and radiation pattern dipole has the form shown in Figure 22.5. Directional pattern is a graphical representation of the distribution of radiation intensity in various directions in the form of a curve constructed so that the length of a ray segment drawn from a dipole in a certain direction to a point on the curve is proportional to the radiation intensity.
Calculations also show that power
R dipole radiation is proportional to the square of the second time derivative of the dipole moment
:
Because the
, (22.35)
That average power
turns out proportional to the square of the amplitude of the dipole moment and fourth power of frequency.
On the other hand, considering that 
, we get that the radiation power is proportional to the square of the acceleration:
This statement is true not only for charge oscillations, but also for arbitrary charge movement.
Wave optics
In this section we will consider such light phenomena in which the wave nature of light is manifested. Let us recall that light is characterized by wave-particle duality and there are phenomena that can be explained only on the basis of the idea of light as a flow of particles. But we will consider these phenomena in quantum optics.
General information about light
So, we consider light an electromagnetic wave. In an electromagnetic wave, and oscillates. It has been experimentally established that the physiological, photochemical, photoelectric and other effects of light are determined by the vector of the light wave, which is why it is called light. Accordingly, we will assume that the light wave is described by the equation:
where is the amplitude,
- wave number (wave vector),
Distance along the direction of propagation.
The plane in which it oscillates is called plane of oscillation. A light wave travels at speed
, (2)
called refractive index and characterizes the difference between the speed of light in a given medium and the speed of light in a vacuum (emptiness).
In most cases, transparent substances have magnetic permeability, and the refractive index can almost always be considered to be determined by the dielectric constant of the medium:
Meaning n used to characterize optical density of the medium: the larger n, the more optically dense the medium is called .
Visible light has wavelengths in the range 
and frequencies
| |
Hz Real light receivers are not able to keep track of such fleeting processes and record time-averaged energy flux . A-priory , light intensity is the modulus of the time-averaged value of the energy flux density transferred by a light wave :
(4)
Since in an electromagnetic wave
, (6)
Ι ~ ~ ~ (7)
I ~ A 2(8)
Rays we will call the lines along which light energy propagates.
The vector of the average energy flow is always directed tangentially to the beam. In isotropic media coincides in direction with the normal to the wave surfaces.
In natural light there are waves with very different orientations of the plane of vibration. Therefore, despite the transverse nature of light waves, the radiation of conventional light sources does not exhibit asymmetry with respect to the direction of propagation. This feature of (natural) light is explained by the following: the resulting light wave from the source is composed of waves emitted by various atoms. Each atom emits a wave within seconds. During this time, space is formed wave train (a sequence of “humps and troughs”) approximately 3 meters long.
The plane of oscillation of each train is quite definite. But at the same time, a huge number of atoms emit their trains, and the plane of vibration of each train is oriented independently of the others, in a random manner. That's why in the resulting wave from the body oscillations in different directions are represented with equal probability. It means that, if you use some device to study the intensity of light with different vector orientations, then in natural light the intensity does not depend on the orientation .
Measuring intensity is a long process compared to the period of the wave, and the considered ideas about the nature of natural light are convenient when describing fairly long processes.
However, at a given moment in time at a specific point in space, as a result of the addition of vectors of individual trains, a certain specific one is formed. Due to random “switching on” and “switching off” of individual atoms a light wave excites at a given point an oscillation close to a harmonic one, but the amplitude, frequency and phase of the oscillations depend on time and change chaotically. The orientation of the oscillation plane also changes chaotically yy. Thus, oscillations of the light vector at a given point in the medium can be described by the equation:
(9)
Moreover, and there are functions chaotically varying in time ii. This idea of natural light is convenient if time periods comparable to the period of a light wave are considered.
Light in which the directions of vector oscillations are ordered in some way is called polarized.
If oscillations of the light vector occur only in one plane passing through the beam, then the light is called flat - or linearly polarized. In other words, in plane polarized light the plane of vibration has a strictly fixed position. Other types of ordering are also possible, that is, types of polarization of light.
Huygens' principle
In the geometric optics approximation, light should not penetrate into the geometric shadow region. In fact, light penetrates into this area, and this phenomenon becomes more significant the smaller the obstacles. If the dimensions of the holes or slits are comparable to the wavelength, then geometric optics is not applicable.
Qualitatively, the behavior of light behind an obstacle is explained by Huygens' principle, which makes it possible to construct the wave front at an instant from a known position at an instant.
According to Huygens' principle, each point to which wave motion reaches becomes a point source of secondary waves. The envelope along the fronts of the secondary waves gives the position of the wave front.
Interference of light
Let at some point in the medium two waves (plane polarized) excite two oscillations same frequency and same direction:
And 
. (24.14)
The amplitude of the resulting oscillation is determined by the expression:
For incoherent waves, it changes randomly and all values are equally probable. Therefore, from (24.15) it follows:
6 If the waves are coherent and , then
But it depends on , - the length of the path from the wave sources to a given point and different for different points in the environment. Hence, when coherent waves are superimposed, a redistribution of the light flux in space occurs, as a result of which the light intensity increases at some points in the medium, , and decreases at others - . This phenomenon is called interference.
The absence of interference in everyday life when using several light sources is explained by their incoherence. Individual atoms emit pulses for c and the length of the train is ≈ 3 meters. For the new train, not only is the orientation of the plane of polarization random, but the phase is also unpredictable.
In reality, coherent waves are obtained by dividing the radiation of one source into two parts. When parts are superimposed, interference can be observed. But in this case, the separation of optical lengths should not be on the order of the length of the train. Otherwise there will be no interference, because various trains are superimposed.
Let separation occur at point O, and superposition at point P. Oscillations are excited at P.
And 
(24.17)
Velocity of wave propagation in relevant media.
Separate phases at a point R:
where is the wavelength of light in vacuum.
The value, i.e. equal to the difference in optical path lengths between the points under consideration is called optical path difference.
then , in (24.16) is equal to unity, and the light intensity in will be maximum.
(24.20)
That 
, oscillations at a point occur in antiphase, which means the light intensity is minimal.
COHERENCE
Coherence – coordinated occurrence of two or more wave processes. There is never absolute consistency, so we can talk about varying degrees of coherence.
There are temporal and spatial coherence.
Temporal coherence
Real Wave Equation
We considered the interference of waves described by equations of the form:
(1)
However, such waves are a mathematical abstraction, since the wave described by (1) must be infinite in time and space. Only in this case can quantities be definite constants.
A real wave, resulting from the superposition of trains from various atoms, contains components whose frequencies lie in a finite frequency range (respectively, wave vectors in ), and A and a experience continuous chaotic changes. Oscillations excited at some point by overlapping real waves, can be described by the expression:
And 
(2)
Moreover, the chaotic changes in functions over time in (2) are independent.
For simplicity of analysis, we assume that the wave amplitudes are constant and identical (this condition is experimentally implemented quite simply):
Changes in frequency and phase can be reduced to changes in frequency only or phase only. Indeed, let us assume that the inharmonicity of functions (2) is due to phase jumps. But, according to what can be proven in mathematics Fourier's theorem, any non-harmonic function can be represented as a sum of harmonic components, the frequencies of which are contained in some . In the limiting case, the sum goes into an integral: any finite and integrable function can be represented by the Fourier integral:
, (3)
Where is the amplitude of the harmonic component of the frequency, analytically determined by the relation:
(4)
So, a function that is non-harmonic due to a change in phase can be represented as a superposition of harmonic components with frequencies at some .
On the other hand, a function with variable frequency and phase can be reduced to a function with only phase variable:
Therefore, to tame further analysis, we will assume:
i.e. we implement phase approach to the concept of “Temporal coherence”.
Equal slope strips
Let a thin plane-parallel plate be illuminated by diffuse monochromatic light. Place a collecting lens parallel to the plate, in its focal plane - screen. Scattered light contains rays from a wide variety of directions. Rays incident at an angle produce 2 reflected rays, which will converge at point . This is true for all rays incident on the surface of the plate at a given angle, at all points on the plate. The lens ensures that all such rays converge to one point, since parallel rays incident on the lens at a certain angle are collected by it at one point of the focal plane, i.e. on the screen. At point O the optical axis of the lens intersects the screen. At this point, rays running parallel to the optical axis are collected.
Rays incident at an angle , but not in the plane of the drawing, but in other planes, will converge at points located at the same distance from the point as the point . As a result of the interference of these rays, a circle with a certain intensity of incident light is formed at a certain distance from the point. Rays incident at a different angle form a circle on the screen with a different illumination, which depends on their optical path difference. As a result, alternating dark and light stripes in the shape of circles are formed on the screen. Each of the circles is formed by rays incident at a certain angle, and they are called stripes of equal slope. These bands are localized at infinity.
The role of the lens can be played by the lens, and the role of the screen can be played by the retina. In this case, the eye must be accommodated to infinity. In white light, multi-colored stripes are obtained.
Stripes of equal thickness
Let's take a wedge-shaped plate. Let it fall on her parallel beam of light. Let us consider the rays reflected from the upper and lower faces of the plate. If these rays are brought together by a lens at a point, they will interfere. With a small angle between the plate faces, the difference in the path of the rays can be calculated using the form 
le for a plane-parallel plate. The rays formed from the incidence of the beam at some other point of the plate will be collected by the lens at the point. The difference in their stroke is determined by the thickness of the plate in the corresponding place. It can be proven that all points of type P lie in the same plane passing through the vertex of the wedge.
If you position the screen so that it is conjugate with the surface in which the points P, P 1 P 2 lie, then a system of light and dark stripes will appear on it, each of which is formed due to reflections from the plate in places of a certain thickness. Therefore, in this case the stripes are called stripes of equal thickness.
When observed in white light, the stripes will be colored. Bands of equal thickness are localized near the surface of the plate. At normal incidence of light - on the surface.
In real conditions, when observing the coloring of soap and oil films, mixed stripes are observed.
Diffraction of light.
27.1. Diffraction of light
Diffractioncalled a set of phenomena observed in a medium with sharp optical inhomogeneities and associated with deviations in the propagation of light from the laws of geometric optics .
To observe diffraction, an opaque barrier is placed along the path of a light wave from a certain source, covering part of the wave surface of the wave emitted by the source. The resulting diffraction pattern is observed on a screen located along the continuation of the rays.
There are two types of diffraction. If the rays coming from the source and from the obstacle to the observation point can be considered almost parallel, then they say thatFraunhofer diffraction, or diffraction in parallel beams. If the Fraunhofer diffraction conditions are not met,talk about Fresnel diffraction.
It is necessary to clearly understand that there is no fundamental physical difference between interference and diffraction. Both phenomena are caused by the redistribution of energy of overlapping coherent light waves. Usually when considering a finite number discrete sources light, then they talk about interference . If the superposition of waves from coherent sources continuously distributed in space then they talk about diffraction .
27.2. Huygens–Fresnel principle
Huygens' principle allows, in principle, to explain the penetration of light into the region of a geometric shadow, but does not say anything about the intensity of waves propagating in different directions. Fresnel supplemented Huygens' principle with an indication of how the intensity of radiation from a wave surface element in different directions should be calculated, as well as with an indication that secondary waves are coherent, and when calculating the intensity of light at a certain point, it is necessary to take into account the interference of secondary waves. .
