The concept of degree in mathematics is introduced in the 7th grade in algebra class. And subsequently, throughout the entire course of studying mathematics, this concept is actively used in its various forms. Degrees are a rather difficult topic, requiring memorization of values and the ability to count correctly and quickly. To work with degrees faster and better, mathematicians came up with degree properties. They help to reduce large calculations, convert a huge example into a single number to some extent. There are not so many properties, and all of them are easy to remember and apply in practice. Therefore, the article discusses the basic properties of the degree, as well as where they are applied.
Properties of degree
We will look at 12 properties of degrees, including properties of degrees with the same bases, and give an example for each property. Each of these properties will help you solve problems with degrees faster, and will also save you from numerous computational errors.
1st property.
Many people very often forget about this property and make mistakes, representing a number to the zero power as zero.
2nd property.
3rd property.
It must be remembered that this property can only be used when multiplying numbers; it does not work with a sum! And we must not forget that this and the following properties apply only to powers with the same bases.
4th property.
If a number in the denominator is raised to a negative power, then when subtracting, the degree of the denominator is taken in parentheses to correctly change the sign in further calculations.
The property only works when dividing, it does not apply when subtracting!
5th property.
6th property.
This property can also be applied in the opposite direction. A unit divided by a number to some extent is that number to the minus power.
7th property.
This property cannot be applied to sum and difference! Raising a sum or difference to a power uses abbreviated multiplication formulas rather than power properties.
8th property.
9th property.
This property works for any fractional power with a numerator equal to one, the formula will be the same, only the power of the root will change depending on the denominator of the power.
This property is also often used in reverse. The root of any power of a number can be represented as this number to the power of one divided by the power of the root. This property is very useful in cases where the root of a number cannot be extracted.
10th property.
This property works not only with square roots and second powers. If the degree of the root and the degree to which this root is raised coincide, then the answer will be a radical expression.
11th property.
You need to be able to see this property in time when solving it in order to save yourself from huge calculations.
12th property.
Each of these properties will come across you more than once in tasks; it can be given in its pure form, or it may require some transformations and the use of other formulas. Therefore, to make the right decision, it is not enough to know only the properties; you need to practice and incorporate other mathematical knowledge.
Application of degrees and their properties
They are actively used in algebra and geometry. Degrees in mathematics have a separate, important place. With their help, exponential equations and inequalities are solved, and equations and examples related to other branches of mathematics are often complicated by powers. Powers help to avoid large and lengthy calculations; powers are easier to abbreviate and calculate. But to work with large powers, or with powers of large numbers, you need to know not only the properties of the power, but also work competently with bases, be able to expand them to make your task easier. For convenience, you should also know the meaning of numbers raised to a power. This will reduce your time when solving, eliminating the need for lengthy calculations.
The concept of degree plays a special role in logarithms. Since the logarithm, in essence, is a power of a number.
Abbreviated multiplication formulas are another example of the use of powers. The properties of degrees cannot be used in them; they are expanded according to special rules, but in each formula of abbreviated multiplication there are invariably degrees.
Degrees are also actively used in physics and computer science. All conversions to the SI system are made using powers, and in the future, when solving problems, the properties of the power are used. In computer science, powers of two are actively used for the convenience of counting and simplifying the perception of numbers. Further calculations for converting units of measurement or calculations of problems, just like in physics, occur using the properties of degrees.
Degrees are also very useful in astronomy, where you rarely see the use of the properties of a degree, but the degrees themselves are actively used to shorten the notation of various quantities and distances.
Degrees are also used in everyday life, when calculating areas, volumes, and distances.
Degrees are used to record very large and very small quantities in any field of science.
Exponential equations and inequalities
Properties of degrees occupy a special place precisely in exponential equations and inequalities. These tasks are very common, both in school courses and in exams. All of them are solved by applying the properties of degree. The unknown is always found in the degree itself, so knowing all the properties, solving such an equation or inequality is not difficult.
If you need to raise a specific number to a power, you can use . Now we will take a closer look at properties of degrees.
Exponential numbers open up great possibilities, they allow us to transform multiplication into addition, and adding is much easier than multiplying.
For example, we need to multiply 16 by 64. The product of multiplying these two numbers is 1024. But 16 is 4x4, and 64 is 4x4x4. That is, 16 by 64 = 4x4x4x4x4, which is also equal to 1024.
The number 16 can also be represented as 2x2x2x2, and 64 as 2x2x2x2x2x2, and if we multiply, we again get 1024.
Now let's use the rule. 16=4 2, or 2 4, 64=4 3, or 2 6, at the same time 1024=6 4 =4 5, or 2 10.
Therefore, our problem can be written differently: 4 2 x4 3 =4 5 or 2 4 x2 6 =2 10, and each time we get 1024.
We can solve a number of similar examples and see that multiplying numbers with powers reduces to adding exponents, or exponential, of course, provided that the bases of the factors are equal.
Thus, without performing multiplication, we can immediately say that 2 4 x2 2 x2 14 = 2 20.
This rule is also true when dividing numbers with powers, but in this case the exponent of the divisor is subtracted from the exponent of the dividend. Thus, 2 5:2 3 =2 2, which in ordinary numbers is equal to 32:8 = 4, that is, 2 2. Let's summarize:
a m x a n =a m+n, a m: a n =a m-n, where m and n are integers.
At first glance it may seem that this is multiplying and dividing numbers with powers not very convenient, because first you need to represent the number in exponential form. It is not difficult to represent the numbers 8 and 16, that is, 2 3 and 2 4, in this form, but how to do this with the numbers 7 and 17? Or what to do in cases where a number can be represented in exponential form, but the bases for exponential expressions of numbers are very different. For example, 8x9 is 2 3 x 3 2, in which case we cannot sum the exponents. Neither 2 5 nor 3 5 are the answer, nor does the answer lie in the interval between these two numbers.
Then is it worth bothering with this method at all? Definitely worth it. It provides enormous benefits, especially for complex and time-consuming calculations.
Articles on science and mathematics
Properties of powers with the same bases
There are three properties of degrees with the same bases and natural exponents. This
- Work sum
- Private two powers with the same bases is equal to the expression where the base is the same and the exponent is difference indicators of the original factors.
- Raising a number to a power is equal to an expression in which the base is the same number and the exponent is work two degrees.
Be careful! Rules regarding addition and subtraction degrees with the same bases does not exist.
Let us write these properties-rules in the form of formulas:
- a m ? a n = a m+n
- a m ? a n = a m–n
- (a m) n = a mn
Now let's look at them using specific examples and try to prove them.
5 2 ? 5 3 = 5 5 - here we applied the rule; Now let’s imagine how we would solve this example if we didn’t know the rules:
5 2 ? 5 3 = 5 ? 5 ? 5 ? 5 ? 5 = 5 5 - five squared is five times five, and cubed is the product of three fives. The result is the product of five fives, but this is something other than five to the fifth power: 5 5 .
3 9 ? 3 5 = 3 9–5 = 3 4. Let's write the division as a fraction:
It can be shortened: 
As a result we get: 
Thus, we proved that when dividing two powers with the same bases, their exponents must be subtracted.
However, when dividing, the divisor cannot be equal to zero (since you cannot divide by zero). In addition, since we consider degrees only with natural exponents, we cannot, as a result of subtracting exponents, obtain a number less than 1. Therefore, the formula a m? a n = a m–n restrictions are imposed: a ? 0 and m > n.
Let's move on to the third property:
(2 2) 4 = 2 2?4 = 2 8
Let's write it in expanded form:
(2 2) 4 = (2 ? 2) 4 = (2 ? 2) ? (2 ? 2) ? (2 ? 2) ? (2 ? 2) = 2 ? 2 ? 2 ? 2 ? 2 ? 2 ? 2 ? 2 = 2 8
You can come to this conclusion by reasoning logically. You need to multiply two squared four times. But there are two twos in each square, which means there will be eight twos in total.
scienceland.info
Rules for addition and subtraction.
1. Changing the places of the terms does not change the sum (commutative property of addition)
13+25=38, can be written as: 25+13=38
2. The result of addition will not change if adjacent terms are replaced by their sum (associative property of addition).
10+13+3+5=31 can be written as: 23+3+5=31; 26+5=31; 23+8=31, etc.
3. Units add up to ones, tens add up to tens, etc.
34+11=45 (3 tens plus 1 more ten; 4 units plus 1 unit).
4. Units are subtracted from units, tens from tens, etc.
53-12=41 (3 units minus 2 units; 5 tens minus 1 ten)
note: 10 ones make one ten. This must be remembered when subtracting, because if the number of units of the subtrahend is greater than that of the minuend, then we can “borrow” one ten from the minuend.
41-12 = 29 (In order to subtract 1 from 2, we must first “borrow” one from tens, we get 11-2 = 9; remember that the one being reduced has 1 less ten, therefore, 3 tens remain and from it 1 ten is subtracted. Answer 29).
5. If you subtract one of them from the sum of two terms, you get the second term.
This means that addition can be checked using subtraction.
To check, subtract one of the terms from the sum: 49-7=42 or 49-42=7
If, as a result of subtraction, you did not receive one of the terms, then an error was made in your addition.
6. If you add the subtrahend to the difference, you get the minuend.
This means that subtraction can be checked by addition.
To check, add the subtrahend to the difference: 19+50=69.
If, as a result of the procedure described above, you did not receive the subtraction, then an error was made in your subtraction.
Adding and subtracting rational numbers
This lesson covers addition and subtraction of rational numbers. The topic is classified as complex. Here it is necessary to use the entire arsenal of previously acquired knowledge.
The rules for adding and subtracting integers also apply to rational numbers. Recall that rational numbers are numbers that can be represented as a fraction, where a – this is the numerator of the fraction, b is the denominator of the fraction. Moreover b should not be zero.
In this lesson, we will increasingly call fractions and mixed numbers by one common phrase - rational numbers.
Lesson navigation:
Example 1. Find the value of an expression
Let's enclose each rational number in brackets along with its signs. We take into account that the plus given in the expression is an operation sign and does not apply to a fraction. This fraction has its own plus sign, which is invisible due to the fact that it is not written down. But we will write it down for clarity:
This is the addition of rational numbers with different signs. To add rational numbers with different signs, you need to subtract the smaller one from the larger module, and prefix the resulting answer with the sign whose module is greater. And in order to understand which modulus is greater and which is smaller, you need to be able to compare the moduli of these fractions before calculating them:
The modulus of a rational number is greater than the modulus of a rational number. Therefore, we subtracted from . We received an answer. Then, reducing this fraction by 2, we got the final answer.
If desired, some primitive actions, such as enclosing numbers in brackets and adding modules, can be skipped. This example can be written briefly:
![]()
Example 2. Find the value of an expression
Let's enclose each rational number in brackets along with its signs. We take into account that the minus given in the expression is a sign of the operation and does not apply to a fraction.
The fraction in this case is a positive rational number with a plus sign that is invisible. But we will write it down for clarity:

Let's replace subtraction with addition. Let us remind you that to do this you need to add the opposite number to the minuend of the subtrahend:
We obtained the addition of negative rational numbers. To add negative rational numbers, you need to add their modules and put a minus in front of the resulting answer:
Example 3. Find the value of an expression
In this expression, the fractions have different denominators. To make our task easier, let’s reduce these fractions to the same (common) denominator. We will not dwell on this in detail. If you are having difficulty, be sure to go back to the lesson on operating with fractions and repeat it.
After reducing the fractions to a common denominator, the expression will take the following form:
This is the addition of rational numbers with different signs. We subtract the smaller module from the larger module and put in front of the resulting answer the sign whose module is greater:
Example 4. Find the value of an expression

We got a sum of three terms. First, let's find the value of the expression, then add to the resulting answer
First action:

Second action:
Thus, the value of the expression is equal to.
The solution for this example can be written briefly
Example 5. Find the value of an expression
Let's enclose each number in brackets along with its signs. To do this, let’s temporarily expand the mixed number
Let's calculate the integer parts:
In the main expression, instead of ![]() Let's write down the resulting unit:
Let's write down the resulting unit:
Let's collapse the resulting expression. To do this, omit the parentheses and write the unit and fraction together
The solution for this example can be written briefly:
Example 6. Find the value of an expression
Let's convert the mixed number to an improper fraction. Let's rewrite the rest as is:
Let's enclose each rational number in brackets along with its signs:

Let's replace subtraction with addition:

We obtained the addition of negative rational numbers. Let's add up the modules of these numbers and put a minus in front of the resulting answer:
Thus, the value of the expression is .
The solution for this example can be written briefly:
Example 7. Find the value of an expression
Let's write the mixed number in expanded form. Let's rewrite the rest as it is:
![]()
We enclose each rational number in brackets together with its signs

Let's replace subtraction with addition where possible:

Let's calculate the integer parts:
In the main expression, instead of writing the resulting number?7

The expression is an expanded form of writing a mixed number. You can immediately write down the answer by writing down the numbers?7 and the fraction together (hiding the minus of this fraction)

So the value of the expression is
The solution for this example can be written much shorter. If we skip some details, it can be written as follows:
Example 8. Find the value of an expression
This expression can be calculated in two ways. Let's look at each of them.
First way. The integer and fractional parts of the expression are evaluated separately.
First, let's write mixed numbers in expanded form:
Let's enclose each number in brackets along with its signs:
Let's replace subtraction with addition where possible:
We got a sum of several terms. According to the combinatory law of addition, if an expression contains several terms, then the sum will not depend on the order of actions. This will allow us to group the integer and fractional parts separately:
Let's calculate the integer parts:
In the main expression, instead of writing the resulting number?3
Let's calculate the fractional parts:
In the main expression, instead of writing the resulting mixed number
To evaluate the resulting expression, you must temporarily expand the mixed number, then put parentheses around each number and replace the subtraction with addition. This must be done very carefully so as not to confuse the signs of the terms.
After transforming the expression, we got a new expression that is easy to calculate. A similar expression was in example 7. Let us recall that we added the integer parts separately and left the fractional part as is:
So the value of the expression is
The solution for this example can be written briefly
The short solution skips the steps of putting numbers in brackets, replacing subtraction with addition, and adding modules. If you are in school or another educational institution, then you will be required to skip these primitive actions in order to save time and space. The short solution above can be written even shorter. It will look like this:
Therefore, when you are at school or another educational institution, be prepared for the fact that some actions will have to be performed in your mind.
Second way. Mixed number expressions are converted to improper fractions and calculated like ordinary fractions.
Let us enclose each rational number in brackets along with its signs
Let's replace subtraction with addition:
Now let’s convert mixed numbers into improper fractions:
We obtained the addition of negative rational numbers. Let’s add up their modules and put a minus in front of the resulting answer:
We received the same answer as last time.
The detailed solution for the second method is as follows:
Example 9. Find expression expressions 
First way. Let's add the whole and fractional parts separately.
This time we’ll try to skip some primitive actions, such as writing an expression in expanded form, enclosing numbers in brackets, replacing subtraction with addition, and adding modules:

Please note that fractional parts have been reduced to a common denominator.
Second way. Let's convert mixed numbers into improper fractions and calculate them like ordinary fractions.
Example 10. Find the value of an expression 
Let's replace subtraction with addition:

The resulting expression does not contain negative numbers, which are the main reason for errors. And since there are no negative numbers, we can remove the plus in front of the subtrahend and also remove the parentheses. Then we get the simplest expression that is easy to calculate:
In this example, the integer and fractional parts were calculated separately.
Example 11. Find the value of an expression
This is the addition of rational numbers with different signs. Let us subtract the smaller one from the larger module and put in front of the resulting number the sign whose module is greater:
Example 12. Find the value of an expression 
The expression consists of several parameters. According to the order of actions, you need to perform the actions in brackets first.
First, we calculate the expression, then we add the resulting answers.
First action:

Second action:

Third action:

Answer: expression value  equals
equals
Example 13. Find the value of an expression 
Let's replace subtraction with addition:
Obtained by adding rational numbers with different signs. Let's subtract the smaller one from the larger module and put in front of the answer the sign whose module is larger. But we are dealing with mixed numbers. To understand which modulus is greater and which is smaller, you need to compare the moduli of these mixed numbers. And to compare the moduli of mixed numbers, you need to convert them to improper fractions and compare them like ordinary fractions.
The following figure shows all the stages of comparing moduli of mixed numbers
Having found out which module is larger and which is smaller, we can continue calculating our example:
Thus, the meaning of the expression  equals
equals
Let's look at the addition and subtraction of decimal fractions, which also belong to rational numbers and which can be both positive and negative.
Example 14. Find the value of the expression?3.2 + 4.3
Let's enclose each rational number in brackets along with its signs. We take into account that the plus given in the expression is an operation sign and does not apply to the decimal fraction 4.3. This decimal fraction has its own plus sign, which is invisible due to the fact that it is not written down. But we will write it down for clarity:
This is the addition of rational numbers with different signs. To add rational numbers with different signs, you need to subtract the smaller one from the larger module, and prefix the resulting answer with the sign whose module is greater. And in order to understand which module is larger and which is smaller, you need to be able to compare the modules of these decimal fractions before calculating them:
The modulus of the number 4.3 is greater than the modulus of the number ?3.2, so we subtracted 3.2 from 4.3. We received the answer 1.1. The answer is positive, since the answer must contain the sign of the larger module, that is, the module |+4,3|.
Thus, the value of the expression?3.2 + (+4.3) is 1.1
Example 15. Find the value of the expression 3.5 + (?8.3)
This is the addition of rational numbers with different signs. As in the previous example, subtract the smaller one from the larger module and put in front of the answer the sign whose module is greater
3,5 + (?8,3) = ?(|?8,3| ? |3,5|) = ?(8,3 ? 3,5) = ?(4,8) = ?4,8
Thus, the value of the expression 3.5 + (?8.3) is equal to?4.8
This example can be written briefly:
Example 16. Find the value of the expression?7,2 + (?3,11)
This is the addition of negative rational numbers. To add negative rational numbers, you need to add their modules and put a minus in front of the resulting answer. You can skip the entry with modules so as not to clutter the expression:
7,2 + (?3,11) = ?7,20 + (?3,11) = ?(7,20 + 3,11) = ?(10,31) = ?10,31
Thus, the value of the expression?7.2 + (?3.11) is equal to?10.31
This example can be written briefly:
Example 17. Find the value of the expression?0.48 + (?2.7)
This is the addition of negative rational numbers. Let's add up their modules and put a minus sign in front of the resulting answer. You can skip the entry with modules so as not to clutter the expression:
0,48 + (?2,7) = (?0,48) + (?2,70) = ?(0,48 + 2,70) = ?(3,18) = ?3,18
Example 18. Find the value of the expression?4,9 ? 5.9
Let's enclose each rational number in brackets along with its signs. We take into account that the minus given in the expression is a sign of the operation and does not apply to the decimal fraction 5.9. This decimal fraction has its own plus sign, which is invisible due to the fact that it is not written down. But we will write it down for clarity:
Let's replace subtraction with addition:
We obtained the addition of negative rational numbers. Add up their modules and put a minus in front of the resulting answer. You can skip the entry with modules so as not to clutter the expression:
(?4,9) + (?5,9) = ?(4,9 + 5,9) = ?(10,8) = ?10,8
Thus, the value of the expression is ?4.9 ? 5.9 equals?10.8
= ?(4,9 + 5,9) = ?(10,8) = ?10,8
Example 19. Find the value of the expression 7? 9.3
Let's put each number in brackets along with its signs
Let's replace subtraction with addition
We obtained the addition of rational numbers with different signs. Let's subtract the smaller one from the larger module and put in front of the answer the sign whose module is larger. You can skip the entry with modules so as not to clutter the expression:
(+7) + (?9,3) = ?(9,3 ? 7) = ?(2,3) = ?2,3
Thus, the value of the expression 7 ? 9.3 equals?2.3
The detailed solution to this example is written as follows:
7 ? 9,3 = (+7) ? (+9,3) = (+7) + (?9,3) = ?(|?9,3| ? |+7|) =
A short solution would look like this:
Example 20. Find the value of the expression?0.25 ? (?1,2)
Let's replace subtraction with addition:
We obtained the addition of rational numbers with different signs. Let us subtract the smaller module from the larger module and put in front of the answer the sign whose module is greater:
0,25 + (+1,2) = |+1,2| ? |?0,25| = 1,2 ? 0,25 = 0,95
The detailed solution to this example is written as follows:
0,25 ? (?1,2) = (?0,25) + (+1,2) = |+1,2| ? |?0,25| = 1,2 ? 0,25 = 0,95
A short solution would look like this:
Example 21. Find the value of the expression?3.5 + (4.1 ? 7.1)
First of all, let's perform the actions in brackets, then add the resulting answer with the number?3.5. We will skip the entry with modules so as not to clutter up the expressions.
First action:
4,1 ? 7,1 = (+4,1) ? (+7,1) = (+4,1) + (?7,1) = ?(7,1 ? 4,1) = ?(3,0) = ?3,0
Second action:
3,5 + (?3,0) = ?(3,5 + 3,0) = ?(6,5) = ?6,5
Answer: the value of the expression?3.5 + (4.1 ? 7.1) is equal to?6.5.
3,5 + (4,1 ? 7,1) = ?3,5 + (?3,0) = ?6,5
Example 22. Find the value of the expression (3.5 ? 2.9)? (3.7 ? 9.1)
Let's perform the actions in brackets, then from the number that was obtained as a result of executing the first brackets, subtract the number that was obtained as a result of executing the second brackets. We will skip the entry with modules so as not to clutter up the expressions.
First action:
3,5 ? 2,9 = (+3,5) ? (+2,9) = (+3,5) + (?2,9) = 3,5 ? 2,9 = 0,6
Second action:
3,7 ? 9,1 = (+3,7) ? (+9,1) = (+3,7) + (?9,1) = ?(9,1 ? 3,7) = ?(5,4) = ?5,4
Third act
0,6 ? (?5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6
Answer: value of the expression (3.5 ? 2.9) ? (3.7 ? 9.1) equals 6.
A short solution to this example can be written as follows:
(3,5 ? 2,9) ? (3,7 ? 9,1) = 0,6 ? (?5,4) = 6,0 = 6
Example 23. Find the value of the expression?3.8 + 17.15 ? 6.2? 6.15
Let us enclose each rational number in brackets along with its signs
Replace subtraction with addition where possible
The expression consists of several terms. According to the combinatory law of addition, if an expression consists of several terms, then the sum will not depend on the order of actions. This means that the terms can be added in any order.
Let's not reinvent the wheel, but add up all the terms from left to right in the order they appear:
First action:
(?3,8) + (+17,15) = 17,15 ? 3,80 = 13,35
Second action:
13,35 + (?6,2) = 13,35 ? ?6,20 = 7,15
Third action:
7,15 + (?6,15) = 7,15 ? 6,15 = 1,00 = 1
Answer: value of the expression?3.8 + 17.15 ? 6.2? 6.15 equals 1.
A short solution to this example can be written as follows:
3,8 + 17,15 ? 6,2 ? 6,15 = 13,35 + (?6,2) ? 6,15 = 7,15 ? 6,15 = 1,00 = 1
Short solutions create fewer problems and confusion, so it is advisable to get used to them.
Example 24. Find the value of an expression
Let's convert the decimal fraction?1.8 to a mixed number. We'll rewrite the rest as it is. If you have difficulty converting a decimal into a mixed number, be sure to review the decimals lesson.
![]()
Example 25. Find the value of an expression ![]()
Let's replace subtraction with addition. At the same time, let’s convert the decimal fraction (?4,4) into an improper fraction

There are no negative numbers in the resulting expression. And since there are no negative numbers, we can remove the plus in front of the second number and omit the parentheses. Then we get a simple expression for addition, which can be easily solved
Example 26. Find the value of an expression ![]()
Let's convert the mixed number into an improper fraction, and the decimal fraction?0.85 into a common fraction. We get the following expression:

We obtained the addition of negative rational numbers. Let's add up their modules and put a minus sign in front of the resulting answer. You can skip the entry with modules so as not to clutter the expression:

Example 27. Find the value of an expression 
Let's convert both fractions to improper fractions. To convert the decimal 2.05 to an improper fraction, you can convert it first to a mixed number and then to an improper fraction:
![]()
After converting both fractions to improper fractions, we get the following expression:

We obtained the addition of rational numbers with different signs. Let us subtract the smaller module from the larger module and put in front of the resulting answer the sign whose module is greater:

Example 28. Find the value of an expression
Let's replace subtraction with addition. At the same time, let’s convert the decimal fraction to a common fraction
Example 29. Find the value of an expression 
Let's convert the decimal fractions ?0.25 and ?1.25 into ordinary fractions, and leave the rest as is. We get the following expression:

You can first replace subtraction with addition where possible and add rational numbers one after another. There is a second option: first add the rational numbers and , and then subtract the rational number from the resulting number. We will use this option.
First action:
Second action:
Answer: expression value  equal to?2.
equal to?2.
Example 30. Find the value of an expression

Let's convert decimal fractions to ordinary fractions. Let's leave the rest as is

We got a sum of several terms. If the sum consists of several terms, then the expression can be evaluated in any order. This follows from the associative law of addition.
Therefore, we can organize the most convenient option for us. First of all, you can add the first and last terms, namely the rational numbers and . These numbers have the same denominators, which means this will free us from the need to reduce them to it.
First action:

The resulting number can be added to the second term, namely a rational number. Rational numbers have identical denominators in their fractional parts, which again is an advantage for us
Second action:

Well, let’s add the resulting number?7 with the last term, namely the rational number. Conveniently, when calculating this expression, the sevens will disappear, that is, their sum will be equal to zero, since the sum of opposite numbers is zero
Third action:

Answer: the value of the expression is
Did you like the lesson?
Join our new VKontakte group and start receiving notifications about new lessons
Adding and subtracting integers
In this lesson we will learn adding and subtracting integers, as well as rules for their addition and subtraction.
Recall that integers are all positive and negative numbers, as well as the number 0. For example, the following numbers are integers:
Positive numbers are easy to add and subtract, multiply and divide. Unfortunately, the same cannot be said about negative numbers, which confuse many beginners with their minuses in front of each number. As practice shows, mistakes made due to negative numbers frustrate students the most.
Examples of adding and subtracting integers
The first thing you should learn is to add and subtract integers using a coordinate line. It is not at all necessary to draw a coordinate line. It is enough to imagine it in your thoughts and see where the negative numbers are located and where the positive ones are.
Let's consider the simplest expression: 1 + 3. The value of this expression is 4:
This example can be understood using a coordinate line. To do this, from the point where the number 1 is located, you need to move three steps to the right. As a result, we will find ourselves at the point where the number 4 is located. In the figure you can see how this happens:
The plus sign in the expression 1 + 3 tells us that we should move to the right in the direction of increasing numbers.
Example 2. Let's find the value of the expression 1? 3.
The value of this expression is?2
This example can again be understood using a coordinate line. To do this, from the point where the number 1 is located, you need to move to the left three steps. As a result, we will find ourselves at the point where the negative number?2 is located. In the picture you can see how this happens:
Minus sign in expression 1? 3 tells us that we should move to the left in the direction of decreasing numbers.
In general, you need to remember that if addition is carried out, then you need to move to the right in the direction of increase. If subtraction is carried out, then you need to move to the left in the direction of decrease.
Example 3. Find the value of the expression?2 + 4
The value of this expression is 2
This example can again be understood using a coordinate line. To do this, from the point where the negative number?2 is located, you need to move four steps to the right. As a result, we will find ourselves at the point where the positive number 2 is located.
It can be seen that we have moved from the point where the negative number?2 is located to the right side by four steps and ended up at the point where the positive number 2 is located.
The plus sign in the expression ?2 + 4 tells us that we should move to the right in the direction of increasing numbers.
Example 4. Find the value of the expression?1 ? 3
The value of this expression is?4
This example can again be solved using a coordinate line. To do this, from the point where the negative number?1 is located, you need to move to the left three steps. As a result, we will find ourselves at the point where the negative number is located?4
It can be seen that we have moved from the point where the negative number?1 is located to the left side by three steps and ended up at the point where the negative number?4 is located.
The minus sign in the expression?1 ? 3 tells us that we should move to the left in the direction of decreasing numbers.
Example 5. Find the value of the expression?2 + 2
The value of this expression is 0
This example can be solved using a coordinate line. To do this, from the point where the negative number?2 is located, you need to move to the right two steps. As a result, we will find ourselves at the point where the number 0 is located
It can be seen that we have moved from the point where the negative number?2 is located to the right side by two steps and ended up at the point where the number 0 is located.
The plus sign in the expression ?2 + 2 tells us that we should move to the right in the direction of increasing numbers.
Rules for adding and subtracting integers
To calculate this or that expression, it is not necessary to imagine a coordinate line every time, much less draw it. It is more convenient to use ready-made rules.
When applying the rules, you need to pay attention to the sign of the operation and the signs of the numbers that need to be added or subtracted. This will determine which rule to apply.
Example 1. Find the value of the expression?2 + 5
Here a positive number is added to a negative number. In other words, numbers with different signs are added. ?2 is a negative number, and 5 is a positive number. For such cases, the following rule is provided:
So, let's see which module is bigger:

The modulus of the number 5 is greater than the modulus of the number?2. The rule requires subtracting the smaller one from the larger module. Therefore, we must subtract 2 from 5, and before the resulting answer put the sign whose modulus is greater.
The number 5 has a larger modulus, so the sign of this number will be in the answer. That is, the answer will be positive:
Usually written shorter? 2 + 5 = 3
Example 2. Find the value of the expression 3 + (?2)
Here, as in the previous example, numbers with different signs are added. 3 is a positive number, and ?2 is negative. Please note that the number?2 is enclosed in parentheses to make the expression clearer and prettier. This expression is much easier to understand than the expression 3+?2.
So, let's apply the rule for adding numbers with different signs. As in the previous example, we subtract the smaller module from the larger module and before the answer we put the sign whose module is larger:
3 + (?2) = |3| ? |?2| = 3 ? 2 = 1
The modulus of the number 3 is greater than the modulus of the number?2, so we subtracted 2 from 3, and before the resulting answer we put the modulus sign that is greater. The number 3 has a larger modulus, which is why the sign of this number is included in the answer. That is, the answer is positive.
Usually written shorter 3 + (?2) = 1
Example 3. Find the value of expression 3? 7
In this expression, a larger number is subtracted from a smaller number. For such a case, the following rule is provided:
To subtract a larger number from a smaller number, you need to subtract the smaller number from the larger number and put a minus in front of the resulting answer.
There is a slight catch to this expression. Let us remember that the equal sign (=) is placed between quantities and expressions when they are equal to each other.
The value of the expression 3? 7 how did we find out it’s equal?4. This means that any transformations that we will perform in this expression must be equal?4
But we see that at the second stage there is an expression 7? 3, which is not equal to?4.

To correct this situation, the expression 7 ? 3 must be put in brackets and a minus sign must be placed in front of this bracket:
3 ? 7 = ? (7 ? 3) = ? (4) = ?4
In this case, equality will be observed at each stage:

After the expression has been evaluated, the parentheses can be removed, which is what we did.
So to be more precise the solution should look like this:
3 ? 7 = ? (7 ? 3) = ? (4) = ? 4
This rule can be written using variables. It will look like this:
a? b = ? (b ? a)
A large number of parentheses and operation signs can complicate the solution of a seemingly simple problem, so it is more advisable to learn how to write such examples briefly, for example 3 ? 7 = ? 4.
In fact, adding and subtracting integers comes down to nothing more than addition. What does this mean? This means that if you need to subtract numbers, this operation can be replaced by addition.
So let's get acquainted with the new rule:
Subtracting one number from another means adding to the minuend a number that is opposite to the one being subtracted.
For example, consider the simplest expression 5? 3. At the initial stages of studying mathematics, we simply put an equal sign and wrote down the answer:
But now we are progressing in our study, so we need to adapt to the new rules. The new rule says that subtracting one number from another means adding to the minuend a number that is opposite to the one being subtracted.
Let's try to understand this rule using the example of the expression 5?3. The minuend in this expression is 5, and the subtrahend is 3. The rule says that in order to subtract 3 from 5, you need to add to 5 a number that is the opposite of 3. The opposite of 3 is the number?3. Let's write a new expression:
And we already know how to find meanings for such expressions. This is the addition of numbers with different signs, which we discussed above. To add numbers with different signs, you need to subtract the smaller one from the larger module, and before the resulting answer put the sign whose module is greater:
5 + (?3) = |5| ? |?3| = 5 ? 3 = 2
The modulus of the number 5 is greater than the modulus of the number?3. Therefore, we subtracted 3 from 5 and got 2. The number 5 has a larger modulus, so we put the sign of this number in the answer. That is, the answer is positive.
At first, not everyone is able to quickly replace subtraction with addition. This is due to the fact that positive numbers are written without their plus sign.
For example, in the expression 3? The 1 minus sign indicating subtraction is an operation sign and does not refer to one. The unit in this case is a positive number and it has its own plus sign, but we don’t see it, since a plus is traditionally not written before positive numbers.
Therefore, for clarity, this expression can be written as follows:
For convenience, numbers with their own signs are placed in brackets. In this case, replacing subtraction with addition is much easier. The subtracted number in this case is the number (+1), and the opposite number is (?1). Let's replace the subtraction operation with addition and instead of the subtrahend (+1) we write the opposite number (?1)
(+3) ? (+1) = (+3) + (?1) = |+3| ? |?1| = 3 ? 1 = 2
At first glance, it might seem like there’s no point in these extra movements if you can use the good old method to put an equal sign and immediately write down the answer 2. In fact, this rule will help us out more than once.
Let's solve the previous example 3? 7, using the subtraction rule. First, let's bring the expression to normal form, assigning each number its own signs. Three has a plus sign because it is a positive number. The minus sign indicating subtraction does not apply to seven. Seven has a plus sign because it is also a positive number:
Let's replace subtraction with addition:
Further calculation is not difficult:
Example 7. Find the value of the expression?4 ? 5
Again we have a subtraction operation. This operation must be replaced by addition. To the minuend (?4) we add the number opposite to the subtrahend (+5). The opposite number for the subtrahend (+5) is the number (?5).
We have come to a situation where we need to add negative numbers. For such cases, the following rule is provided:
To add negative numbers, you need to add their modules and put a minus in front of the resulting answer.
So, let’s add up the modules of numbers, as the rule requires us to do, and put a minus in front of the resulting answer:
(?4) ? (+5) = (?4) + (?5) = |?4| + |?5| = 4 + 5 = ?9
The entry with modules must be enclosed in brackets and a minus sign must be placed before these brackets. This way we will provide a minus that should appear before the answer:
(?4) ? (+5) = (?4) + (?5) = ?(|?4| + |?5|) = ?(4 + 5) = ?(9) = ?9
The solution for this example can be written briefly:
Example 8. Find the value of the expression?3 ? 5 ? 7? 9
Let's bring the expression to a clear form. Here, all numbers except number?3 are positive, so they will have plus signs:
Let us replace subtraction operations with addition operations. All minuses (except for the minus, which is in front of the three) will change to pluses and all positive numbers will change to the opposite:
Now let's apply the rule for adding negative numbers. To add negative numbers, you need to add their modules and put a minus in front of the resulting answer:
= ?(|?3| + |?5| + |?7| + |?9|) = ?(3 + 5 + 7 + 9) = ?(24) = ?24
The solution for this example can be written briefly:
3 ? 5 ? 7 ? 9 = ?(3 + 5 + 7 + 9) = ?24
Example 9. Find the value of the expression?10 + 6? 15 + 11? 7
Let's bring the expression to a clear form:
There are two operations here: addition and subtraction. We leave the addition as it is, and replace the subtraction with addition:
(?10) + (+6) ? (+15) + (+11) ? (+7) = (?10) + (+6) + (?15) + (+11) + (?7)
Following the order of actions, we will perform each action in turn, based on the previously learned rules. Entries with modules can be skipped:
First action:
(?10) + (+6) = ? (10 ? 6) = ? (4) = ? 4
Second action:
(?4) + (?15) = ? (4 + 15) = ? (19) = ? 19
Third action:
(?19) + (+11) = ? (19 ? 11) = ? (8) = ?8
Fourth action:
(?8) + (?7) = ? (8 + 7) = ? (15) = ? 15
Thus, the value of the expression?10 + 6? 15 + 11? 7 equals?15
Note. It is not at all necessary to bring the expression into a understandable form by enclosing numbers in parentheses. When habituation to negative numbers occurs, this step can be skipped because it is time-consuming and can be confusing.
So, to add and subtract integers, you need to remember the following rules:
To add numbers with different signs, you need to subtract the smaller module from the larger module, and before the resulting answer put the sign whose module is larger.
To subtract a larger number from a smaller number, you need to subtract the smaller number from the larger number and put a minus sign in front of the resulting answer.
Subtracting one number from another means adding to the one being reduced the opposite number of the one being subtracted.
To add negative numbers, you need to add their modules and put a minus sign in front of the resulting answer.
- Hockey without rules VKontakte The game was released in September 2012, and has already gained almost 700,000 users. There are two game modes and many possibilities for team building. The flow of a match in Hockey Without Rules VKontakte is reminiscent of the early games in the NHL series from Electronic Arts. 3 players per […]
- Poker rules Omaha Hold'em Omaha Hi-Lo and five-card Omaha Omaha Hold'Em is a slight modification of Texas Hold'em. If you are new to this most popular form of poker, study the rules of Texas Hold'em here; knowledge of them is necessary to understand the rules of Omaha . All […]
- Solving genetics problems using Mendel's 1st and 2nd laws Lecture 8 Julia Kjahrenova 1. - presentation The presentation was published 3 years ago by Alina Artemyeva Similar presentations Presentation on the topic: "Solving genetics problems using Mendel's 1st and 2nd laws Lecture 8 Julia Kjahrenova 1 " […]
- 5-7 algebra rules A numerical sequence, each member of which, starting from the second, is equal to the previous one, added to the same number d for a given sequence, is called an arithmetic progression. The number d is called the difference of an arithmetic progression. In arithmetic progression, i.e. in […]
- We determine the transport tax rate for vans and other atypical cars with category “B” We catch the necessary information from the PTS Let’s say right away that the data specified in line 4 “Vehicle category (A, B, C, D, trailer)” of the vehicle passport (PTS) ), does not need to be taken into account. After all, category “B” does not mean […]
- Rating of insurance companies OSAGO OSAGO refers to compulsory insurance; it operates not only in Russia, but also in other neighboring countries. These policies are issued by many insurance companies that have received the appropriate license to conduct such activities. However, […]
- Accommodation hotel Ufa Mini-hotel in Ufa 5 Five Rooms We invite guests of the capital to a cozy, comfortable hotel located in the center of Ufa on Komsomolskaya street 159/1. In the immediate vicinity of the hotel there is the Iskra IMAX cinema complex, a circus, restaurant-club A cafe, Beer Berry restaurant, shopping center […]
- Rules for using Present Simple Tense in English Present Simple Tense is a grammatical tense that is considered one of the easiest to understand, since the present simple tense exists in all languages. This is true in Slavic languages. If you are reading this article, it means that you only [...]
How to multiply powers? Which powers can be multiplied and which cannot? How to multiply a number by a power?
In algebra, you can find a product of powers in two cases:
1) if the degrees have the same bases;
2) if the degrees have the same indicators.
When multiplying powers with the same bases, the base must be left the same, and the exponents must be added:
When multiplying degrees with the same indicators, the overall indicator can be taken out of brackets:
Let's look at how to multiply powers using specific examples.
The unit is not written in the exponent, but when multiplying powers, they take into account:
When multiplying, there can be any number of powers. It should be remembered that you don’t have to write the multiplication sign before the letter:
In expressions, exponentiation is done first.
If you need to multiply a number by a power, you should first perform the exponentiation, and only then the multiplication:
www.algebraclass.ru
Addition, subtraction, multiplication, and division of powers
Addition and subtraction of powers
It is obvious that numbers with powers can be added like other quantities , by adding them one after another with their signs.
So, the sum of a 3 and b 2 is a 3 + b 2.
The sum of a 3 - b n and h 5 -d 4 is a 3 - b n + h 5 - d 4.
Odds equal powers of identical variables can be added or subtracted.
So, the sum of 2a 2 and 3a 2 is equal to 5a 2.
It is also obvious that if you take two squares a, or three squares a, or five squares a.
But degrees various variables And various degrees identical variables, must be composed by adding them with their signs.
So, the sum of a 2 and a 3 is the sum of a 2 + a 3.
It is obvious that the square of a, and the cube of a, is not equal to twice the square of a, but to twice the cube of a.
The sum of a 3 b n and 3a 5 b 6 is a 3 b n + 3a 5 b 6.
Subtraction powers are carried out in the same way as addition, except that the signs of the subtrahends must be changed accordingly.
Or:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6
Multiplying powers
Numbers with powers can be multiplied, like other quantities, by writing them one after the other, with or without a multiplication sign between them.
Thus, the result of multiplying a 3 by b 2 is a 3 b 2 or aaabb.
Or:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
The result in the last example can be ordered by adding identical variables.
The expression will take the form: a 5 b 5 y 3.
By comparing several numbers (variables) with powers, we can see that if any two of them are multiplied, then the result is a number (variable) with a power equal to amount degrees of terms.
So, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Here 5 is the power of the multiplication result, which is equal to 2 + 3, the sum of the powers of the terms.
So, a n .a m = a m+n .
For a n , a is taken as a factor as many times as the power of n;
And a m is taken as a factor as many times as the degree m is equal to;
That's why, powers with the same bases can be multiplied by adding the exponents of the powers.
So, a 2 .a 6 = a 2+6 = a 8 . And x 3 .x 2 .x = x 3+2+1 = x 6 .
Or:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1
Multiply (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Answer: x 4 - y 4.
Multiply (x 3 + x – 5) ⋅ (2x 3 + x + 1).
This rule is also true for numbers whose exponents are negative.
1. So, a -2 .a -3 = a -5 . This can be written as (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
If a + b are multiplied by a - b, the result will be a 2 - b 2: that is
The result of multiplying the sum or difference of two numbers is equal to the sum or difference of their squares.
If you multiply the sum and difference of two numbers raised to square, the result will be equal to the sum or difference of these numbers in fourth degrees.
So, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.
Division of degrees
Numbers with powers can be divided like other numbers, by subtracting from the dividend, or by placing them in fraction form.
Thus, a 3 b 2 divided by b 2 is equal to a 3.
Writing a 5 divided by a 3 looks like $\frac $. But this is equal to a 2 . In a series of numbers
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
any number can be divided by another, and the exponent will be equal to difference indicators of divisible numbers.
When dividing degrees with the same base, their exponents are subtracted..
So, y 3:y 2 = y 3-2 = y 1. That is, $\frac = y$.
And a n+1:a = a n+1-1 = a n . That is, $\frac = a^n$.
Or:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b + y) n-3
The rule is also true for numbers with negative values of degrees.
The result of dividing a -5 by a -3 is a -2.
Also, $\frac: \frac = \frac .\frac = \frac = \frac $.
h 2:h -1 = h 2+1 = h 3 or $h^2:\frac = h^2.\frac = h^3$
It is necessary to master multiplication and division of powers very well, since such operations are very widely used in algebra.
Examples of solving examples with fractions containing numbers with powers
1. Decrease the exponents by $\frac $ Answer: $\frac $.
2. Decrease exponents by $\frac$. Answer: $\frac$ or 2x.
3. Reduce the exponents a 2 /a 3 and a -3 /a -4 and bring to a common denominator.
a 2 .a -4 is a -2 the first numerator.
a 3 .a -3 is a 0 = 1, the second numerator.
a 3 .a -4 is a -1 , the common numerator.
After simplification: a -2 /a -1 and 1/a -1 .
4. Reduce the exponents 2a 4 /5a 3 and 2 /a 4 and bring to a common denominator.
Answer: 2a 3 /5a 7 and 5a 5 /5a 7 or 2a 3 /5a 2 and 5/5a 2.
5. Multiply (a 3 + b)/b 4 by (a - b)/3.
6. Multiply (a 5 + 1)/x 2 by (b 2 - 1)/(x + a).
7. Multiply b 4 /a -2 by h -3 /x and a n /y -3 .
8. Divide a 4 /y 3 by a 3 /y 2 . Answer: a/y.
Properties of degree
We remind you that in this lesson we will understand properties of degrees with natural indicators and zero. Powers with rational exponents and their properties will be discussed in lessons for 8th grade.
A power with a natural exponent has several important properties that allow us to simplify calculations in examples with powers.
Property No. 1
Product of powers
When multiplying powers with the same bases, the base remains unchanged, and the exponents of the powers are added.
a m · a n = a m + n, where “a” is any number, and “m”, “n” are any natural numbers.
This property of powers also applies to the product of three or more powers.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
(0.8) 3 · (0.8) 12 = (0.8) 3 + 12 = (0.8) 15
Please note that in the specified property we were talking only about the multiplication of powers with the same bases. It does not apply to their addition.
You cannot replace the sum (3 3 + 3 2) with 3 5. This is understandable if
calculate (3 3 + 3 2) = (27 + 9) = 36, and 3 5 = 243
Property No. 2
Partial degrees
When dividing powers with the same bases, the base remains unchanged, and the exponent of the divisor is subtracted from the exponent of the dividend.
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
11 3 − 2 4 2 − 1 = 11 4 = 44
Example. Solve the equation. We use the property of quotient powers.
3 8: t = 3 4
Answer: t = 3 4 = 81
Using properties No. 1 and No. 2, you can easily simplify expressions and perform calculations.
- Example. Simplify the expression.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Example. Find the value of an expression using the properties of exponents.
2 11 − 5 = 2 6 = 64
Please note that in Property 2 we were only talking about dividing powers with the same bases.
You cannot replace the difference (4 3 −4 2) with 4 1. This is understandable if you calculate (4 3 −4 2) = (64 − 16) = 48, and 4 1 = 4
Property No. 3
Raising a degree to a power
When raising a degree to a power, the base of the degree remains unchanged, and the exponents are multiplied.
(a n) m = a n · m, where “a” is any number, and “m”, “n” are any natural numbers.

Please note that property No. 4, like other properties of degrees, is also applied in reverse order.
(a n · b n)= (a · b) n
That is, to multiply powers with the same exponents, you can multiply the bases, but leave the exponent unchanged.
2 4 5 4 = (2 5) 4 = 10 4 = 10,000
0.5 16 2 16 = (0.5 2) 16 = 1
In more complex examples, there may be cases where multiplication and division must be performed over powers with different bases and different exponents. In this case, we advise you to do the following.
For example, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216
An example of raising a decimal to a power.
4 21 (−0.25) 20 = 4 4 20 (−0.25) 20 = 4 (4 (−0.25)) 20 = 4 (−1) 20 = 4 1 = 4
Properties 5
Power of a quotient (fraction)
To raise a quotient to a power, you can raise the dividend and the divisor separately to this power, and divide the first result by the second.
(a: b) n = a n: b n, where “a”, “b” are any rational numbers, b ≠ 0, n - any natural number.
(5: 3) 12 = 5 12: 3 12
We remind you that a quotient can be represented as a fraction. Therefore, we will dwell on the topic of raising a fraction to a power in more detail on the next page.
Powers and roots
Operations with powers and roots. Degree with negative ,
zero and fractional indicator. About expressions that have no meaning.
Operations with degrees.
1. When multiplying powers with the same base, their exponents are added:
a m · a n = a m + n .
2. When dividing degrees with the same base, their exponents are deducted .
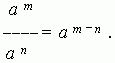
3. The degree of the product of two or more factors is equal to the product of the degrees of these factors.
4. The degree of a ratio (fraction) is equal to the ratio of the degrees of the dividend (numerator) and divisor (denominator):
(a/b) n = a n / b n .
5. When raising a power to a power, their exponents are multiplied:
All the above formulas are read and executed in both directions from left to right and vice versa.
EXAMPLE (2 3 5 / 15)² = 2² · 3² · 5² / 15² = 900 / 225 = 4 .
Operations with roots. In all the formulas below, the symbol means arithmetic root(the radical expression is positive).
1. The root of the product of several factors is equal to the product of the roots of these factors:
2. The root of a ratio is equal to the ratio of the roots of the dividend and the divisor:
![]()
3. When raising a root to a power, it is enough to raise to this power radical number:

4. If you increase the degree of the root by m times and at the same time raise the radical number to the mth power, then the value of the root will not change:
![]()
5. If you reduce the degree of the root by m times and simultaneously extract the mth root of the radical number, then the value of the root will not change:
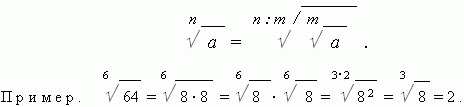
Expanding the concept of degree. So far we have considered degrees only with natural exponents; but operations with powers and roots can also lead to negative, zero And fractional indicators. All these exponents require additional definition.
A degree with a negative exponent. The power of a certain number with a negative (integer) exponent is defined as one divided by the power of the same number with an exponent equal to the absolute value of the negative exponent:

Now the formula a m : a n = a m - n can be used not only for m, more than n, but also with m, less than n .
EXAMPLE a 4: a 7 = a 4 — 7 = a — 3 .
If we want the formula a m : a n = a m — n was fair when m = n, we need a definition of degree zero.
A degree with a zero index. The power of any non-zero number with exponent zero is 1.
EXAMPLES. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.
Degree with a fractional exponent. In order to raise a real number a to the power m / n, you need to extract the nth root of the mth power of this number a:

About expressions that have no meaning. There are several such expressions.
Where a ≠ 0 , does not exist.
In fact, if we assume that x is a certain number, then in accordance with the definition of the division operation we have: a = 0· x, i.e. a= 0, which contradicts the condition: a ≠ 0
— any number.
In fact, if we assume that this expression is equal to some number x, then according to the definition of the division operation we have: 0 = 0 · x. But this equality occurs when any number x, which was what needed to be proven.
0 0 — any number.

Solution. Let's consider three main cases:
1) x = 0 – this value does not satisfy this equation
2) when x> 0 we get: x/x= 1, i.e. 1 = 1, which means
What x– any number; but taking into account that in
in our case x> 0, the answer is x > 0 ;
Rules for multiplying powers with different bases
DEGREE WITH RATIONAL INDICATOR,
POWER FUNCTION IV
§ 69. Multiplication and division of powers with the same bases
Theorem 1. To multiply powers with the same bases, it is enough to add the exponents and leave the base the same, that is
Proof. By definition of degree
2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.
We looked at the product of two powers. In fact, the proven property is true for any number of powers with the same bases.
Theorem 2. To divide powers with the same bases, when the index of the dividend is greater than the index of the divisor, it is enough to subtract the index of the divisor from the index of the dividend, and leave the base the same, that is at t > p
(a =/= 0)
Proof. Recall that the quotient of dividing one number by another is the number that, when multiplied by the divisor, gives the dividend. Therefore, prove the formula where a =/= 0, it's the same as proving the formula
If t > p , then the number t - p will be natural; therefore, by Theorem 1
Theorem 2 is proven.
It should be noted that the formula
we have proved it only under the assumption that t > p . Therefore, from what has been proven, it is not yet possible to draw, for example, the following conclusions:
![]()
In addition, we have not yet considered degrees with negative exponents and we do not yet know what meaning can be given to expression 3 - 2 .
Theorem 3. To raise a degree to a power, it is enough to multiply the exponents, leaving the base of the degree the same, that is
Proof. Using the definition of degree and Theorem 1 of this section, we obtain:

Q.E.D.
For example, (2 3) 2 = 2 6 = 64;
![]()
518 (Oral) Determine X from the equations:
1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;
2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .
519. (Set no.) Simplify:

520. (Set no.) Simplify:
521. Present these expressions in the form of degrees with the same bases:
1) 32 and 64; 3) 8 5 and 16 3; 5) 4 100 and 32 50;
2) -1000 and 100; 4) -27 and -243; 6) 81 75 8 200 and 3 600 4 150.
It is obvious that numbers with powers can be added like other quantities , by adding them one after another with their signs.
So, the sum of a 3 and b 2 is a 3 + b 2.
The sum of a 3 - b n and h 5 -d 4 is a 3 - b n + h 5 - d 4.
Odds equal powers of identical variables can be added or subtracted.
So, the sum of 2a 2 and 3a 2 is equal to 5a 2.
It is also obvious that if you take two squares a, or three squares a, or five squares a.
But degrees various variables And various degrees identical variables, must be composed by adding them with their signs.
So, the sum of a 2 and a 3 is the sum of a 2 + a 3.
It is obvious that the square of a, and the cube of a, is not equal to twice the square of a, but to twice the cube of a.
The sum of a 3 b n and 3a 5 b 6 is a 3 b n + 3a 5 b 6.
Subtraction powers are carried out in the same way as addition, except that the signs of the subtrahends must be changed accordingly.
Or:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 - 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6
Multiplying powers
Numbers with powers can be multiplied, like other quantities, by writing them one after the other, with or without a multiplication sign between them.
Thus, the result of multiplying a 3 by b 2 is a 3 b 2 or aaabb.
Or:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
The result in the last example can be ordered by adding identical variables.
The expression will take the form: a 5 b 5 y 3.
By comparing several numbers (variables) with powers, we can see that if any two of them are multiplied, then the result is a number (variable) with a power equal to amount degrees of terms.
So, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Here 5 is the power of the result of the multiplication, equal to 2 + 3, the sum of the powers of the terms.
So, a n .a m = a m+n .
For a n , a is taken as a factor as many times as the power of n;
And a m is taken as a factor as many times as the degree m is equal to;
That's why, powers with the same bases can be multiplied by adding the exponents of the powers.
So, a 2 .a 6 = a 2+6 = a 8 . And x 3 .x 2 .x = x 3+2+1 = x 6 .
Or:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1
Multiply (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Answer: x 4 - y 4.
Multiply (x 3 + x - 5) ⋅ (2x 3 + x + 1).
This rule is also true for numbers whose exponents are negative.
1. So, a -2 .a -3 = a -5 . This can be written as (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
If a + b are multiplied by a - b, the result will be a 2 - b 2: that is
The result of multiplying the sum or difference of two numbers is equal to the sum or difference of their squares.
If you multiply the sum and difference of two numbers raised to square, the result will be equal to the sum or difference of these numbers in fourth degrees.
So, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.
Division of degrees
Numbers with powers can be divided like other numbers, by subtracting from the dividend, or by placing them in fraction form.
Thus, a 3 b 2 divided by b 2 is equal to a 3.
Or:
$\frac(9a^3y^4)(-3a^3) = -3y^4$
$\frac(a^2b + 3a^2)(a^2) = \frac(a^2(b+3))(a^2) = b + 3$
$\frac(d\cdot (a - h + y)^3)((a - h + y)^3) = d$
Writing a 5 divided by a 3 looks like $\frac(a^5)(a^3)$. But this is equal to a 2 . In a series of numbers
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
any number can be divided by another, and the exponent will be equal to difference indicators of divisible numbers.
When dividing degrees with the same base, their exponents are subtracted..
So, y 3:y 2 = y 3-2 = y 1. That is, $\frac(yyy)(yy) = y$.
And a n+1:a = a n+1-1 = a n . That is, $\frac(aa^n)(a) = a^n$.
Or:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b + y) n-3
The rule is also true for numbers with negative values of degrees.
The result of dividing a -5 by a -3 is a -2.
Also, $\frac(1)(aaaaa) : \frac(1)(aaa) = \frac(1)(aaaaa).\frac(aaa)(1) = \frac(aaa)(aaaaa) = \frac (1)(aa)$.
h 2:h -1 = h 2+1 = h 3 or $h^2:\frac(1)(h) = h^2.\frac(h)(1) = h^3$
It is necessary to master multiplication and division of powers very well, since such operations are very widely used in algebra.
Examples of solving examples with fractions containing numbers with powers
1. Reduce the exponents by $\frac(5a^4)(3a^2)$ Answer: $\frac(5a^2)(3)$.
2. Decrease the exponents by $\frac(6x^6)(3x^5)$. Answer: $\frac(2x)(1)$ or 2x.
3. Reduce the exponents a 2 /a 3 and a -3 /a -4 and bring to a common denominator.
a 2 .a -4 is a -2 the first numerator.
a 3 .a -3 is a 0 = 1, the second numerator.
a 3 .a -4 is a -1 , the common numerator.
After simplification: a -2 /a -1 and 1/a -1 .
4. Reduce the exponents 2a 4 /5a 3 and 2 /a 4 and bring to a common denominator.
Answer: 2a 3 /5a 7 and 5a 5 /5a 7 or 2a 3 /5a 2 and 5/5a 2.
5. Multiply (a 3 + b)/b 4 by (a - b)/3.
6. Multiply (a 5 + 1)/x 2 by (b 2 - 1)/(x + a).
7. Multiply b 4 /a -2 by h -3 /x and a n /y -3 .
8. Divide a 4 /y 3 by a 3 /y 2 . Answer: a/y.
9. Divide (h 3 - 1)/d 4 by (d n + 1)/h.