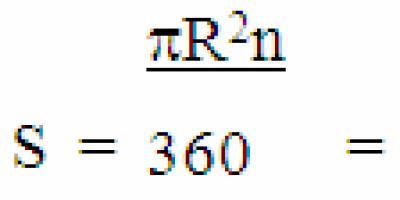In order to illustrate the application of the laws of rigid body dynamics, let us solve the problem of rolling a cylinder down an inclined plane (Fig. 10.5).

Solid mass cylinder m and radius R rolls down an inclined plane without slipping. The angle of inclination of the plane is a, and the height N (N » R). The initial speed of the cylinder is zero. Let's determine the rolling time - T and the velocity of the center of mass of the cylinder at the base of the inclined plane.

When a cylinder rolls, three forces act on it: gravity, elastic support reaction force and friction force peace(after all, rolling without slipping!).

Let's imagine this movement as the sum of two movements: translational with speed V C, with which the cylinder axis moves, and the cylinder rotates around the axis with angular velocity w.

Rice. 10.5

This connection between the speeds of translational and rotational movements follows from the condition “movement without slipping”.

Having differentiated equation (10.9) with respect to time, we obtain the ratio of the angular and linear accelerations of the cylinder:

That is .

Using the theorem on the motion of the center of mass point, we describe the translational motion of the cylinder:

To describe rotation, we use the basic equation of the dynamics of rotational motion:

M C= I C×e. (10.11)

Projecting equation (10.10) onto the directions of the axes x And y, we get two scalar equations:

x: mg Sina – F tr = ma C ; (10.12)

y: N – mgсosa = 0. (10.13)

Let us now turn to equation (10.11). Of the three named forces, the moment relative to the cylinder axis is created only by the friction force:

The moment of inertia of a solid cylinder relative to its axis is equal to (see lecture No. 9):

Taking all this into account, we rewrite equation (10.11) as follows:

Solving equations (10.12) and (10.14) together, we obtain the following values ​​of the unknown quantities:

From equation (10.15) it follows that as the angle of inclination a increases, the static friction force should also increase F tr. But, as you know, its growth is limited by a limiting value:

Since the static friction force (10.15) cannot exceed the limit value (10.17), then the inequality must be satisfied:

⅓mg Sina ≤ m mg Cosa.

It follows that rolling will occur without slipping until the angle a exceeds the value a before:

apre = arctg3m.

Here m is the coefficient of friction of the cylinder along the plane.

The linear acceleration of the cylinder (10.16) is a constant value, therefore, the translational motion of the cylinder is uniformly accelerated. With such a movement without an initial speed, the cylinder will reach the base of the inclined plane in time:

Here: l= - length of the plane;

a=, (see 10.16).

So the rolling time is:

Let's calculate the final speed of translational motion of the cylinder axis:

Note that this problem can be solved more simply by using the law of conservation of mechanical energy.

True, there is a frictional force in the system, but its work is zero, since the point of application of this force during the descent process remains stationary: after all, the movement occurs without slipping. Since there is no work done by the friction force, the mechanical energy of the system does not change.

Let's consider the energy of the cylinder at the initial moment - at the height h and at the end of the descent. The total energy of the cylinder in these positions is the same:

Let us remember that and . Then the equation of the law of conservation of energy can be rewritten as follows:

From here we can easily find the final speed of the cylinder:

which brilliantly confirms our earlier result (10.19).

Lecture 11 “Elements of fluid mechanics”

Lecture outline

1. Fluid pressure. Laws of hydrostatics.

2. Stationary fluid flow. Flow continuity equation.

3. Basic law of dynamics for an ideal fluid. Bernoulli's equation.

4. Application of the Bernoulli equation to solve problems of hydrodynamics.

4.1. Flow of liquid from a vessel.

4.2. Manometric flow meter.

Sterlitamak

Study of bodies rolling down an inclined plane

Goal of the work : acquire some skills in independent research of physical phenomena and processing of the results obtained.

Equipment and accessories : inclined plane (tribometer), scale ruler, set of bodies, scales, stopwatch.

Exercise. Investigate the rolling of cylinders and a ball along an inclined plane.

Note: If a cylinder or ball rolls down an inclined plane located at a slight angle to the horizontal, then the rolling occurs without slipping. If the angle of inclination of the plane exceeds a certain limit value, then rolling will occur with slipping.

When performing the task, it is necessary to determine the limiting angle at which the rolling of bodies begins to occur with slipping. Based on the results of the study, compile a report that reflects the research methodology, provide a table of observation results and give an explanation why, at an angle exceeding a certain value, the rolling of bodies occurs with slipping.

In addition, the task includes determining the moment of inertia of the cylinders and the ball based on the results of observations of their rolling down an inclined plane.

Brief theory

Suppose a cylinder rolls down an inclined plane without slipping. The cylinder is acted upon by external forces: gravity, friction force, and reaction force from the plane. We consider the movement as translational with a speed equal to the speed of the center of mass, and rotational relative to the axis passing through the center of mass.

Equation for the motion of the center of mass of a ball (cylinder)

or in scalar form in projections:

to OX axis: .

to the op-amp axis:

Equation of moments about an axis

When there is no slippage

Let us find the acceleration that the cylinder acquires under the action of the indicated forces. It can be found by using the expression for the kinetic energy of a rolling body

,

(1)

where is the mass of the ball (cylinder), is the translational speed of the center of mass, is the moment of inertia of the ball, relative to the axis of rotation, is the angular velocity of rotation, relative to the axis of rotation.

The change in the kinetic energy of a body is equal to the work of external forces acting on the body. The elementary work of the friction force and reaction of the plane is equal to zero, because their lines of action pass through the instantaneous axis of rotation (). Consequently, the change in the kinetic energy of the body occurs only due to the work of gravity

where is the final speed of the center of mass at the end of the inclined plane, is the initial speed, it is equal to zero, therefore

,

(6)

where is the time of the body rolling down an inclined plane, is the radius of the ball (cylinder), is the mass of the ball (cylinder), is the angle of inclination of the plane to the horizon, is the length of the inclined plane.

By measuring the above values, you can calculate the moment of inertia of the rolling cylinder. It can be solid, hollow, with grooves on its forming surface, etc. Formula (9): valid for both cylinders and a ball.

Carry out the experiment with each of the bodies at least three times. The results of observations and calculations are included in Table 1.

Table 1

No.	Rolling body shape	Weight, kg	Radius, m	Length of inclined plane (m)	Rolling time, s	Moment of inertia, kg m 2

Determine for each case the error in determining .

Determine the value of the moment of inertia for each body theoretically. Compare the values ​​of the moment of inertia of bodies determined theoretically and from experiment, and if they do not coincide, explain the reason.

Control questions

1. Define torque. Write in vector form. What is the direction of the torque relative to the force? What is the radius vector of the force? Draw and show in the picture.

2.What direction do angular acceleration and angular velocity have?

3. Define the moment of inertia of a material point and an absolutely rigid body. Physical meaning of inertia.

4. Derive the moment of inertia of the ball and cylinder.

5. Prove Steiner's theorem.

6. Formulate the law of conservation of energy during rotational motion.

7. Derive the formula for calculating kinetic energy taking into account the rotation of the body.

8. Derive the law of conservation of angular momentum of a system of bodies.

9. Define the center of mass of the heat system.

10.Formulate the conditions under which a body rolls without slipping and derive the formulas used in the calculation.

11.Formulate the laws of dynamics for rotational motion and derive them for a material point and for an absolutely rigid body.

12.Explain how the measurement error in the work was calculated.

MINISTRY OF EDUCATION AND SCIENCE OF THE RF

BRANCH OF FSBEI HPE "UFA STATE AVIATION TECHNICAL UNIVERSITY"

IN THE CITY OF STERLITAMAK

Guidelines

for laboratory work in the course of general physics

section: section: "Mechanics. Mechanical vibrations. Statistical physics and thermodynamics"

LABORATORY WORK No. 9

Determination of the coefficient
internal friction of liquids

Sterlitamak

Goal of the work: determine the coefficient of internal friction of an unknown fluid using the Stokes method.

Instruments and equipment: glass cylinder with the test liquid, stopwatch, balls of different diameters, micrometer.

Brief theory

Any body moving in a viscous fluid is subject to a drag force. In the general case, the magnitude of this force depends on many factors: on the internal friction of the fluid, on the shape of the body, on the nature of the flow, etc.

The force of internal friction that arises during macroscopic movements in a liquid is directly proportional to the velocity gradient. The proportionality coefficient is called the coefficient of internal friction, or simply the viscosity of the liquid. Viscosity (or dynamic viscosity) is numerically equal to the force of internal friction acting per unit area of ​​the interface of parallel moving layers of liquid, when the speed of their movement decreases by one when moving in the direction perpendicular to the boundary, per unit length, i.e. ~ at .

.

(1)

Law (1) was obtained by Newton from an analysis of experimental data and was the basis for studying the movement of viscous liquids and gases.

As an example, consider the uniform motion of a small ball of liquid radius.

Let us denote the speed of the ball relative to the fluid by .

The distribution of velocities in adjacent layers of liquid entrained by the ball should have the form shown in Figure 1. In the immediate vicinity of the surface of the ball, this velocity is equal to , and with distance it decreases and practically becomes equal to zero at some distance from the surface. Obviously, the larger the radius of the ball, the greater the mass of liquid involved in its motion, and must be proportional to

The surface of the ball and the total frictional force experienced by the moving ball is equal to

Formula (5) is called Stokes' law.

The Stokes formula is applicable only in the case of bodies of sufficiently small sizes and low speeds of their motion. At high speeds, complex vortex movements of the fluid arise around moving bodies, and the drag force increases in proportion to the square of the speed, and not to its first power.

The role of friction is characterized by a dimensionless quantity called the Reynolds number:

,

where are the linear dimensions characteristic of the fluid flow under consideration. In the case of fluid flow through a pipe, - the radius of the pipe, - the average speed. The ratio is called the kinematic viscosity coefficient.

In order to explain the role of the Reynolds number, consider a fluid volume element with edge length . The kinetic energy of this volume is equal to:

The frictional force acting on a fluid volume element is proportional to its surface area, viscosity coefficient, and velocity gradient. Assuming that the velocity drops to zero at a distance equal in order of magnitude (in the case of flow through a pipe - in the radial direction), we obtain that the velocity gradient is equal to . Thus, the friction force

The role of friction in fluid flow is small if the work is small compared to the kinetic energy of the fluid volume, that is, if the inequality is satisfied

,

But - Re is the Reynolds number.

Thus, the role of friction forces during fluid flow is small at high Reynolds numbers.

Let's consider the free fall of a ball in a viscous fluid. The ball is acted upon by 3 forces: gravity, Archimedean force, and drag force, which depends on speed. Let's find the equation of motion of a ball in a liquid. According to Newton's second law

where is the volume of the ball; - its density; - liquid density; - acceleration of gravity.

Solving this equation, we find

.

(9)

As can be seen from (7), the speed of the ball exponentially approaches the steady speed. The establishment of speed is determined by a quantity that has the dimension of time and is called relaxation time. If the fall time is several times longer than the relaxation time, the process of establishing velocity can be considered completed.

By experimentally measuring the steady-state speed of falling of the ball and the value , we can determine the coefficient of internal friction of the liquid using the formula

,

(10)

following from (8).

Note: balls with different radii move in the liquid at equal speeds and with different relaxation times. If, over the entire range of encountered velocities and relaxation times, the values ​​calculated by formula (10) turn out to be the same, then formula (5) correctly conveys the dependence of forces on the radius of the ball. Dependence or independence on serves as a sensitive indicator of the correctness of the theory and the reliability of the experiment. It makes sense to process the results of the experiment only if the value does not show a systematic dependence on . If such a dependence is observed, it is most often due to the influence of the vessel walls.

3. What does the Reynolds number characterize?

4. Laminar and turbulent flow and their connection with the Reynolds number.

5. What are the limits of applicability of Stokes' law?

6. What methods for determining friction force exist?

7. How to explain the mechanism of the phenomenon of viscous friction?

8. What physical quantities does friction depend on?

9. What energy transformations occur when bodies move taking into account the friction force?

10. What is the magnitude of the static and sliding friction force?

11. Explain sliding, static, viscous and rolling friction.

12. Why is sliding friction greater than rolling friction?

13. Why is viscous friction less than sliding friction?

14. How does friction manifest itself in nature? When does it play a positive or negative role? How to get rid of friction?

1) Trofimova T.I. Physics course: textbook for engineering and technical specialties at universities - M.: Academia, 2006.

2) Alexandrov I.V. and others. Modern physics [Electronic resource]: a textbook for students of all forms of education studying in technical and technological areas and specialties - Ufa: UGATU, 2008.

3) Grinkrug M.S., Vakulyuk A.A. Laboratory workshop in physics [Electronic resource] - St. Petersburg: Lan, 2012.

4) Kalashnikov N.P. Fundamentals of Physics: a textbook for universities: in 2 volumes / N.P. Kalashnikov, M.A. Smondyrev - M.: Bustard, 2007.

DETERMINATION OF THE MOMENT OF INERTIA OF A BODY ROLLING OUT OF AN INCLINED PLANE

TARGET : acquire the skill of calculating the moment of inertia of bodies consisting of simple elements, determine the moment of inertia of the body relative to the instantaneous axis of rotation using calculation and experimental methods

EQUIPMENT : installation, set of bodies, stopwatch

THEORETICAL PART

INSTALLATION DESCRIPTION

The work uses bodies whose axis is a cylindrical rod of radius r. One of the fig. 1) placed on parallel guides 2, forming angles α1 and α2 with the horizon.

If the body is released, it will roll down, reach the bottom point and, moving further by inertia, rise up along the guides. The motion of a body in which the trajectories of all points lie in parallel planes is called planar. Plane motion can be represented in two ways: either as a combination of translational motion of a body at the speed of the center of mass and rotational motion around an axis passing through the center of mass; or as soon as rotational motion around an instantaneous axis of rotation (MOB), the position of which is continuously changing. In our case, this instantaneous Z axis passes through the points of contact of the guides with the moving rod.

DESCRIPTION OF MEASUREMENT METHOD

When rolling the body, falling from a height passes the way l0, and rising by inertia to a height the path passes l. At the bottom point the velocity of translational motion of the center of mass is , and the angular velocity of the body

Where t- time of movement from the top point to the bottom, r - radius of the rod (axis).

The rolling body is acted upon by a moment of resistance force Mtr. Its work on the path l0 is equal to A = Mtrφ where the angular path φ = l0/r.

The law of conservation of energy on the path segment l0 has the form

, (2)

where J is the moment of inertia of the rolling body relative to the MOB, m - body mass, including the mass of the rod.

When a body moves down from a height h0 and rolls into a height h, the work done by the resistance forces along the path ( l + l0) is equal to the loss of potential energy

https://pandia.ru/text/80/147/images/image008_41.gif" width="146 height=48" height="48"> (4)

Here the quantity (α1 and α2) is a constant for a given installation.

The moment of inertia of the body relative to MOB is determined by Steiner’s theorem J = J0 + ma2, (5)

8. What functions are called integrals of motion?

9. List additive integrals of motion.

10. How do you understand the following physical categories: “uniformity of time”, “homogeneity of space”, “isotropy of space” and how do they relate to additive integrals of motion?

CONTROL QUESTIONS

1. What is the method for determining the moment of inertia of a body?

2. Indicate possible systematic measurement errors.

3. Indicate the values ​​of kinetic and potential energy when a body rolls: at the beginning and at the end of the movement, at the bottom point and at an arbitrary point.

4. Describe the nature of body movement along guides. What force creates a moment about the axis of rotation?

5. How is angular velocity ω measured in this work?

6. What quantities are measured to determine the speed ω, the moment of friction forces, the work of friction forces?

7. What equations underlie dynamic methods for determining the moment of inertia?

8. Indicate possible sources of random errors in measurements.

9. A homogeneous cylinder of mass m and radius R rolls without slipping along a horizontal plane. The center of the cylinder moves with speed υ0. Find an expression for determining the kinetic energy of the cylinder.

10. Calculate the angular momentum of the Earth due to its motion around its axis. Compare this moment with the angular momentum caused by the movement of the Earth around the Sun. The Earth is considered to be a homogeneous sphere, and the Earth’s orbit is a circle.

V. M. Zrazhevsky

LABORATORY WORK NO.

ROLLING A SOLID BODY FROM AN INCLINED PLANE

Goal of the work: Verification of the law of conservation of mechanical energy when a rigid body rolls down an inclined plane.

Equipment: inclined plane, electronic stopwatch, cylinders of different masses.

Theoretical information

Let the cylinder have radius R and mass m rolls down an inclined plane forming an angle α with the horizon (Fig. 1). There are three forces acting on the cylinder: gravity P = mg, the force of normal pressure of the plane on the cylinder N and the friction force of the cylinder on the plane F tr. , lying in this plane.

The cylinder participates simultaneously in two types of motion: translational motion of the center of mass O and rotational motion relative to the axis passing through the center of mass.

Since the cylinder remains on the plane during movement, the acceleration of the center of mass in the direction of the normal to the inclined plane is zero, therefore

P∙cosα − N = 0. (1)

The equation for the dynamics of translational motion along an inclined plane is determined by the friction force F tr. and the gravity component along the inclined plane mg∙sinα:

ma = mg∙sinα − F tr. , (2)

Where a– acceleration of the center of gravity of the cylinder along an inclined plane.

The equation for the dynamics of rotational motion relative to an axis passing through the center of mass has the form

Iε = F tr. R, (3)

Where I– moment of inertia, ε – angular acceleration. Moment of gravity and relative to this axis is zero.

Equations (2) and (3) are always valid, regardless of whether the cylinder moves along the plane with sliding or without sliding. But from these equations it is impossible to determine three unknown quantities: F tr. , a and ε, one more additional condition is necessary.

If the friction force is sufficiently large, then the cylinder rolls along an inclined path without slipping. Then the points on the circumference of the cylinder must travel the same path length as the center of mass of the cylinder. In this case, linear acceleration a and angular acceleration ε are related by the relation

a = Rε. (4)

From equation (4) ε = a/R. After substitution into (3) we get

. (5)

Replacing in (2) F tr. on (5), we get

. (6)

From the last relation we determine the linear acceleration

. (7)

From equations (5) and (7) the friction force can be calculated:

. (8)

The friction force depends on the angle of inclination α, gravity P = mg and from attitude I/mR 2. Without friction there will be no rolling.

When rolling without sliding, the static friction force plays a role. The rolling friction force, like the static friction force, has a maximum value equal to μ N. Then the conditions for rolling without sliding will be satisfied if

F tr. ≤ μ N. (9)

Taking into account (1) and (8), we obtain

, (10)

or, finally

. (11)

In the general case, the moment of inertia of homogeneous symmetrical bodies of revolution about an axis passing through the center of mass can be written as

I = kmR 2 , (12)

Where k= 0.5 for a solid cylinder (disk); k= 1 for a hollow thin-walled cylinder (hoop); k= 0.4 for a solid ball.

After substituting (12) into (11), we obtain the final criterion for a rigid body to roll off an inclined plane without slipping:

. (13)

Since when a solid body rolls on a solid surface, the rolling friction force is small, the total mechanical energy of the rolling body is constant. At the initial moment of time, when the body is at the top point of the inclined plane at a height h, its total mechanical energy is equal to potential:

W n = mgh = mgs∙sinα, (14)

Where s– the path traveled by the center of mass.

The kinetic energy of a rolling body consists of the kinetic energy of the translational motion of the center of mass with a speed υ and rotational motion with speed ω relative to an axis passing through the center of mass:

. (15)

When rolling without sliding, the linear and angular velocities are related by the relation

υ = Rω. (16)

Let us transform the expression for kinetic energy (15) by substituting (16) and (12) into it:

Movement on an inclined plane is uniformly accelerated:

. (18)

Let us transform (18) taking into account (4):

. (19)

Solving (17) and (19) together, we obtain the final expression for the kinetic energy of a body rolling along an inclined plane:

. (20)

Description of installation and measurement method

You can study the rolling of a body on an inclined plane using the “plane” unit and the electronic stopwatch SE1, which are part of the modular educational complex MUK-M2.

U
The installation is an inclined plane 1, which can be installed at different angles α to the horizon using screw 2 (Fig. 2). Angle α is measured using scale 3. A cylinder 4 with mass m. The use of two rollers of different weights is provided. The rollers are fixed at the top point of the inclined plane using an electromagnet 5, which is controlled using

electronic stopwatch SE1. The distance traveled by the cylinder is measured by a ruler 6 fixed along the plane. The rolling time of the cylinder is measured automatically using sensor 7, which turns off the stopwatch the moment the roller touches the finishing point.

Work order

1. Loosen screw 2 (Fig. 2), set the plane at a certain angle α to the horizontal. Place roller 4 on an inclined plane.

2. Switch the toggle switch for controlling the electromagnets of the mechanical unit to the “flat” position.

3. Set the stopwatch SE1 to mode 1.

4. Press the start button of the stopwatch. Measure the rolling time.

5. Repeat the experiment five times. Record the measurement results in the table. 1.

6. Calculate the value of mechanical energy before and after rolling. Draw a conclusion.

7. Repeat steps 1-6 for other plane inclination angles.

Table 1

	t i, c	(t i − <t>) 2	ways s, m	Tilt angle	roller, kg	W p, j	W K, J
t(a, n)	<t>	å( t i – <t>) 2	Δ s, m		Δ m, kg

8. Repeat steps 1-7 for the second video. Record the results in the table. 2, similar to table. 1.

9. Draw conclusions based on all the results of the work.

Control questions

1. Name the types of forces in mechanics.

2. Explain the physical nature of friction forces.

3. What is the coefficient of friction? Its size?

4. What factors influence the coefficient of static, sliding, and rolling friction?

5. Describe the general nature of the motion of a rigid body during rolling.

6. What is the direction of the frictional moment when rolling on an inclined plane?

7. Write down a system of equations of dynamics when a cylinder (ball) rolls along an inclined plane.

8. Derive formula (13).

9. Derive formula (20).

10. Sphere and cylinder with the same masses m and equal radii R simultaneously begin to slide down an inclined plane from a height h. Will they simultaneously reach the bottom point ( h = 0)?

11. Explain the reason for the braking of a rolling body.

Bibliography

1. Savelyev, I.V. Course of general physics in 3 volumes. T. 1 / I.V. Savelyev. – M.: Nauka, 1989. – § 41–43.

2. Khaikin, S. E. Physical foundations of mechanics / S. E. Khaikin. – M: Nauka, 1971. – § 97.

3. Trofimova T. I. Physics course / T. I. Trofimova. – M: Higher. school, 1990. – § 16–19.

Dynamics and kinematics are two important branches of physics that study the laws of movement of objects in space. The first considers the forces acting on the body, while the second deals directly with the characteristics of the dynamic process, without delving into the reasons for what caused it. Knowledge of these branches of physics must be used to successfully solve problems involving motion on an inclined plane. Let's look at this issue in the article.

Basic formula of dynamics

Of course, we are talking about the second law, which was postulated by Isaac Newton in the 17th century while studying the mechanical motion of solid bodies. Let's write it in mathematical form:

The action of an external force F¯ causes the appearance of linear acceleration a¯ in a body with mass m. Both vector quantities (F¯ and a¯) are directed in the same direction. The force in the formula is the result of the action on the body of all the forces that are present in the system.

In the case of rotational motion, Newton's second law is written as:

Here M and I are inertia, respectively, α is angular acceleration.

Kinematics formulas

Solving problems involving motion on an inclined plane requires knowledge of not only the main formula of dynamics, but also the corresponding expressions of kinematics. They connect acceleration, speed and distance traveled into equalities. For uniformly accelerated (uniformly decelerated) rectilinear motion, the following formulas are used:

S = v 0 *t ± a*t 2 /2

Here v 0 is the value of the initial velocity of the body, S is the path traveled along a straight path during time t. A "+" sign should be added if the speed of the body increases over time. Otherwise (uniformly slow motion), the “-” sign should be used in the formulas. This is an important point.

If the movement is carried out along a circular path (rotation around an axis), then the following formulas should be used:

ω = ω 0 ± α*t;

θ = ω 0 *t ± α*t 2 /2

Here α and ω are the speed, respectively, θ is the angle of rotation of the rotating body during time t.

Linear and angular characteristics are related to each other by the formulas:

Here r is the radius of rotation.

Movement on an inclined plane: forces

This movement is understood as the movement of an object along a flat surface that is inclined at a certain angle to the horizon. Examples include a block sliding on a board or a cylinder rolling on an inclined sheet of metal.

To determine the characteristics of the type of movement under consideration, it is necessary first of all to find all the forces that act on the body (bar, cylinder). They may be different. In general, these can be the following forces:

• heaviness;
• support reactions;
• and/or slipping;
• thread tension;
• external traction force.

The first three of them are always present. The existence of the last two depends on the specific system of physical bodies.

To solve problems involving movement along an inclined plane, it is necessary to know not only the magnitudes of forces, but also their directions of action. If a body rolls down a plane, the friction force is unknown. However, it is determined from the corresponding system of equations of motion.

Solution method

Solving problems of this type begins with determining the forces and their directions of action. To do this, the force of gravity is first considered. It should be decomposed into two component vectors. One of them should be directed along the surface of the inclined plane, and the second should be perpendicular to it. The first component of gravity, in the case of a body moving downwards, provides its linear acceleration. This happens anyway. The second is equal to All these indicators can have different parameters.

The friction force when moving along an inclined plane is always directed against the movement of the body. When it comes to sliding, the calculations are quite simple. To do this, use the formula:

Where N is the support reaction, µ is the friction coefficient, which has no dimension.

If only these three forces are present in the system, then their resultant along the inclined plane will be equal to:

F = m*g*sin(φ) - µ*m*g*cos(φ) = m*g*(sin(φ) - µ*cos(φ)) = m*a

Here φ is the angle of inclination of the plane to the horizon.

Knowing the force F, we can use Newton's law to determine the linear acceleration a. The latter, in turn, is used to determine the speed of movement along an inclined plane after a known period of time and the distance traveled by the body. If you look into it, you can understand that everything is not so complicated.

In the case when a body rolls down an inclined plane without slipping, the total force F will be equal to:

F = m*g*sin(φ) - F r = m*a

Where F r - It is unknown. When a body rolls, the force of gravity does not create a moment, since it is applied to the axis of rotation. In turn, F r creates the following moment:

Considering that we have two equations and two unknowns (α and a are related to each other), we can easily solve this system, and therefore the problem.

Now let's look at how to use the described technique to solve specific problems.

Problem involving the movement of a block on an inclined plane

The wooden block is at the top of the inclined plane. It is known that it has a length of 1 meter and is located at an angle of 45 o. It is necessary to calculate how long it will take for the block to descend along this plane as a result of sliding. Take the friction coefficient equal to 0.4.

We write Newton's law for a given physical system and calculate the value of linear acceleration:

m*g*(sin(φ) - µ*cos(φ)) = m*a =>

a = g*(sin(φ) - µ*cos(φ)) ≈ 4.162 m/s 2

Since we know the distance that the block must travel, we can write the following formula for the path during uniformly accelerated motion without an initial speed:

Where should we express time and substitute known values:

t = √(2*S/a) = √(2*1/4.162) ≈ 0.7 s

Thus, the time it takes to move along the inclined plane of the block will be less than a second. Note that the result obtained does not depend on body weight.

Problem with a cylinder rolling down a plane

A cylinder with a radius of 20 cm and a mass of 1 kg is placed on a plane inclined at an angle of 30 o. You should calculate its maximum linear speed that it will gain when rolling down a plane if its length is 1.5 meters.

Let's write the corresponding equations:

m*g*sin(φ) - F r = m*a;

F r *r = I*α = I*a/r

The moment of inertia of cylinder I is calculated by the formula:

Let's substitute this value into the second formula, express the friction force F r from it and replace it with the resulting expression in the first equation, we have:

F r *r = 1/2*m*r 2 *a/r = >

m*g*sin(φ) - 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

We found that linear acceleration does not depend on the radius and mass of the body rolling off the plane.

Knowing that the length of the plane is 1.5 meters, we find the time of movement of the body:

Then the maximum speed of movement along the inclined plane of the cylinder will be equal to:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

We substitute all the quantities known from the problem conditions into the final formula, and we get the answer: v ≈ 3.132 m/s.