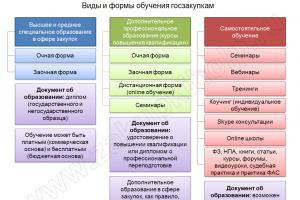
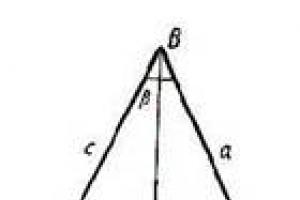
En icke-negativ slumpvariabel har gammafördelning, om dess distributionstäthet uttrycks med formeln
där och , är gammafunktionen:
Således, gammafördelningär en tvåparameterfördelning, den intar en viktig plats i matematisk statistik och tillförlitlighetsteori. Denna fördelning är å ena sidan begränsad.
Om parametern för fördelningskurvans form är ett heltal, beskriver gammafördelningen den tid som krävs för att händelser (misslyckanden) ska inträffa, förutsatt att de är oberoende och uppträder med konstant intensitet .
I de flesta fall beskriver denna fördelning drifttiden för systemet med redundanta fel på åldrande element, återställningstiden för systemet med redundanta fel på åldrande element, återställningstiden för systemet, etc. För olika kvantitativa värden av parametrar antar gammafördelningen en mängd olika former, vilket förklarar dess breda tillämpning. .
Sannolikhetstätheten för gammafördelningen definieras av likheten if
distributionsfunktion. (9)
Observera att tillförlitlighetsfunktionen uttrycks med formeln:
Gammafunktionen har följande egenskaper: , , (11)
därav följer att if är ett icke-negativt heltal, alltså
Dessutom kommer vi i framtiden att behöva ytterligare en egenskap hos gammafunktionen: ; . (13)
Exempel.Återställning av elektronisk utrustning följer lagen om gammafördelning med parametrar och . Bestäm sannolikheten för att återställa hårdvaran per timme.
Lösning. För att bestämma återhämtningssannolikheten använder vi formeln (9) .
För positiva heltalsvärden funktioner och för .
Om vi går över till nya variabler, vars värden kommer att uttryckas; , då får vi tabellintegralen:
I detta uttryck kan lösningen av integralen på höger sida bestämmas med samma formel:
och när kommer
För och kommer de nya variablerna att vara lika med och och själva integralen kommer att vara lika med
Funktionens värde blir
Låt oss hitta de numeriska egenskaperna för en slumpvariabel , beroende på gammafördelningen
I enlighet med jämlikhet (13) får vi . (14)
Det andra initiala momentet hittas av formeln
var . (15)
Observera att vid , minskar felfrekvensen monotont, vilket motsvarar produktens inkörningsperiod. Med ökar felfrekvensen, vilket kännetecknar slitage och åldrande av elementen.
Vid , sammanfaller gammafördelningen med exponentialfördelningen, vid , närmar sig gammafördelningen normallagen. Om det tar värdena av godtyckliga positiva heltal, kallas en sådan gammafördelning Erlang distribution av den e ordningen:
Här räcker det att påpeka att Erlang-lagen -th order summan av oberoende slumpmässiga variabler, som var och en är fördelad enligt en exponentiell lag med en parameter . Erlangs lag ordningen är nära relaterad till det stationära Poisson (enklaste) flödet med intensitet .
Låt det verkligen ske ett sådant flöde av händelser i tiden (Fig. 6).
Ris. 6. Grafisk representation av Poisson-flödet av händelser i tid
Betrakta ett tidsintervall som består av summan intervaller mellan händelser i en sådan ström. Det kan bevisas att en slumpvariabel kommer att följa Erlang-lagen -:e ordningen.
Fördelningstäthet för en stokastisk variabel fördelad enligt Erlang-lagen ordningen, kan uttryckas i termer av en Poisson-fördelningsfunktion i tabellform:
Om värdet multipel av och , då sammanfaller gammafördelningen med chi-kvadratfördelningen.
Observera att fördelningsfunktionen för en slumpvariabel kan beräknas med följande formel:
där bestäms av uttrycken (12) och (13).
Därför har vi följande likheter, som kommer att vara användbara för oss i det följande:
Exempel. Flödet av produkter som produceras på transportören är det enklaste med parametern. Alla tillverkade produkter kontrolleras, defekta placeras i en speciell låda, som inte innehåller mer än produkter är sannolikheten för äktenskap . Bestäm distributionslagen för tidpunkten för fyllning av lådan med defekta produkter och värdet , baserat på det faktum att lådan sannolikt inte kommer att svämma över under skiftet.
Lösning. Intensiteten i det enklaste flödet av defekta produkter kommer att vara . Det är uppenbart att tiden för att fylla lådan med defekta produkter fördelas enligt Erlang-lagen
med parametrar och:
därför (18) och (19): ; .
Antalet defekta artiklar över tiden kommer att fördelas enligt Poissons lag med parametern . Därför önskat antal måste hittas från tillståndet. (20)
Till exempel vid [produkt/h]; ; [h]
från ekvationen för
En slumpvariabel med en Erlang-fördelning har följande numeriska egenskaper(Tabell 6).
Tabell 6
| Sannolikhetstäthet | , , var är skalparametern ; - formulärparameter, distributionsordning, heltal Positivt nummer |
| distributionsfunktion | |
| karakteristisk funktion | |
| Förväntat värde | |
| Mode | |
| Dispersion | |
| Asymmetri | |
| Överskott | |
| Inledande ögonblick | , , , |
| Centrala ögonblick | , |
Observera att en slumpvariabel med en normaliserad Erlang-fördelning av den e ordningen har följande numeriska egenskaper (tabell 7).
Tabell 7
| Sannolikhetstäthet | , , var är skalparametern ; - formulärparameter, distributionsordning, ett positivt heltal |
| distributionsfunktion | |
| karakteristisk funktion | |
| Förväntat värde | |
| Mode | |
| Dispersion | |
| Variationskoefficienten | |
| Asymmetri | |
| Överskott | |
| Inledande ögonblick | , , , |
| Centrala ögonblick | , |
Den här artikeln beskriver formelsyntaxen och användningen av funktionen GAMMA.DIST i Microsoft Excel.
Returnerar gammafördelningen. Denna funktion kan användas för att undersöka variabler som har en skev fördelning. Gammafördelningen används i stor utsträckning vid analys av kösystem.
Syntax
GAMMA.FÖRD(x;alfa;beta;kumulativ)
Syntaxen för funktionen GAMMA.DIST har följande argument:
xär ett obligatoriskt argument. Värdet som du vill beräkna fördelningen för.
Alfaär ett obligatoriskt argument. Fördelningsparameter.
Betaär ett obligatoriskt argument. Fördelningsparameter. Om beta = 1, returnerar GAMMA.DIST standardgammafördelningen.
Väsentligär ett obligatoriskt argument. Booleskt värde som definierar funktionens form. Om det kumulativa argumentet är TRUE returnerar GAMMA.DIST den kumulativa fördelningsfunktionen; om detta argument är FALSK, returneras sannolikhetstäthetsfunktionen.
Anmärkningar
Exempel
Kopiera exempeldata från följande tabell och klistra in den i cell A1 i ett nytt Excel-ark. För att visa formelresultat, välj dem och tryck på F2 följt av ENTER. Ändra bredden på kolumnerna, om det behövs, för att se alla data.
Data | Beskrivning |
|
|---|---|---|
|
Värdet som du vill beräkna fördelningen för |
||
|
Distributionsparameter alfa |
||
|
Distributionsparameter beta |
||
|
Formel |
Beskrivning |
Resultat |
|
GAMMA.DIST(A2;A3;A4;FALSE) |
Sannolikhetstäthet när du använder x-, alfa- och betavärdena i cellerna A2, A3, A4 med integralargument FALSE. |
|
|
GAMMA.DIST(A2;A3;A4;TRUE) |
Den kumulativa fördelningen när du använder x-, alfa- och betavärdena i cellerna A2, A3, A4 med det kumulativa argumentet TRUE. |
Jämn fördelning. kontinuerligt värde X är jämnt fördelat på intervallet ( a, b) om alla dess möjliga värden är i detta intervall och sannolikhetsfördelningstätheten är konstant:
För en slumpmässig variabel X, jämnt fördelad i intervallet ( a, b) (Fig. 4), sannolikheten att falla in i något intervall ( x 1 , x 2) ligger inom intervallet ( a, b), är lika med:
 (30)
(30)
Ris. 4. Graf över den likformiga fördelningstätheten
Exempel jämnt fördelade variablerär avrundningsfel. Så, om alla tabellvärden för en viss funktion är avrundade till samma siffra, och väljer ett slumpmässigt tabellvärde, anser vi att avrundningsfelet för det valda numret är en slumpmässig variabel som är likformigt fördelad i intervallet
exponentiell fördelning. Kontinuerlig slumpvariabel X Det har exponentiell fördelning
 (31)
(31)
Grafen över sannolikhetsfördelningstätheten (31) visas i fig. 5.

Ris. 5. Graf över tätheten av exponentialfördelningen
Tid T felfri drift av ett datorsystem är en slumpvariabel som har en exponentiell fördelning med parametern λ
, fysisk mening vilket är det genomsnittliga antalet fel per tidsenhet, exklusive systemavbrott för reparationer.
Normal (gaussisk) fördelning. Slumpmässigt värde X Det har vanligt (gaussisk) fördelning, om densitetsfördelningen av dess sannolikheter bestäms av beroendet:
 (32)
(32)
Var m = M(X) , .
På normal distribution kallad standard.
Grafen över densiteten för normalfördelningen (32) visas i fig. 6.

Ris. 6. Graf över densiteten för normalfördelningen
Normalfördelningen är den vanligaste fördelningen i olika slumpmässiga naturfenomen. Så, fel i utförandet av kommandon av en automatiserad enhet, utmatningsfel rymdskepp till en given punkt i rymden, fel i datasystems parametrar osv. i de flesta fall har en normal eller nära normalfördelning. Dessutom de slumpvariabler som bildas av summeringen ett stort antal slumpmässiga termer fördelas nästan enligt normallagen.
Gammafördelning. Slumpmässigt värde X Det har gammafördelning, om densitetsfördelningen av dess sannolikheter uttrycks med formeln:
 (33)
(33)
Var  är Eulers gammafunktion.
är Eulers gammafunktion.
Tänk på gammafördelningen, beräkna den förväntat värde, spridning, läge. Med funktionen MS EXCEL GAMMA.DIST() plottar vi fördelningsfunktionen och sannolikhetstäthetsgraferna. Låt oss generera en array av slumptal och uppskatta fördelningsparametrarna.
Gammafördelning(Engelsk) Gammadistribution)
beror på 2 parametrar: r(definierar formen på fördelningen) och λ (definierar skalan). denna fördelning ges av följande formel:
där Г(r) är gammafunktionen: 
om r är ett positivt heltal så är Г(r)=(r-1)!
Anmälningsformuläret ovan distributionstäthet visar tydligt sitt förhållande till. För r=1 Gammafördelning kokar ner till exponentiell fördelning med parametern λ. 
Om parametern λ är ett heltal, då Gammafördelningär summan r oberoende och jämnt fördelade exponentiell lag med parameter λ för slumpvariabler x. Slumpvariabeln alltså y= x 1 + x 2 +… x r Det har gammafördelning med parametrar r och X.
, i sin tur är nära besläktad med diskret . Om Poissonfördelning beskriver antalet slumpmässiga händelser som inträffade under ett visst tidsintervall, alltså exponentiell fördelning, i detta fall beskriver längden på tidsintervallet mellan två på varandra följande händelser.
Av detta följer att till exempel om tiden före den första händelsen beskrivs av exponentiell fördelning med parametern λ, så beskrivs tiden tills den andra händelsen inträffar gammafördelning med r = 2 och samma parameter λ.
Gammafördelning i MS EXCEL
I MS EXCEL används en likvärdig, men annorlunda, form av notation densitet gammafördelning.

Parameter α ( alfa) motsvarar parametern r och parametern b (beta) - parameter 1/A. Nedan kommer vi att hålla oss till just en sådan notation, eftersom detta kommer att göra det lättare att skriva formler.
I MS EXCEL, från och med version 2010, för Distributionsgamma det finns en GAMMA.DIST() funktion, Engelsk titel- GAMMA.DIST(), som låter dig beräkna sannolikhetstäthet(se formeln ovan) och (sannolikheten att en slumpvariabel X har gammafördelning, tar ett värde mindre än eller lika med x).
Notera: Före MS EXCEL 2010 hade EXCEL en funktion GAMMADIST() som låter dig beräkna integrerad distributionsfunktion Och sannolikhetstäthet. GAMMADIST() finns kvar i MS EXCEL 2010 för kompatibilitet.
Funktionsgrafer
Exempelfilen innehåller grafer sannolikhetsfördelningstäthet Och integrerad distributionsfunktion.


Gammafördelning har beteckningen Gamma (alfa; beta).
Notera: För att underlätta att skriva formler i exempelfilen för distributionsparametrar alfa och beta skapade motsvarande.
Notera: Beroende av 2 parametrar gör att du kan bygga distributioner av olika former, vilket utökar tillämpningen av denna fördelning. Gammafördelning, tycka om Exponentiell distribution används ofta för att beräkna väntetiden mellan slumpmässiga händelser. Dessutom är det möjligt att använda denna fördelning för nederbördsmodellering och vägdesign.
Som visas ovan, om parametern alfa= 1, sedan returnerar funktionen GAMMA.DIST() med parametern 1/beta. Om parametern beta= 1, funktionen GAMMA.DIST() returnerar standarden gammafördelning.
Notera: Därför att är ett specialfall gammafördelning, sedan formeln =GAMMA.FÖRD(x,n/2,2,SANT) för ett positivt heltal returnerar n samma resultat som formeln =XI2.DIST(x, n, TRUE) eller =1-XI2.DIST.X(x;n) . Och formeln =GAMMA.FÖRD(x;n/2;2;FALSK) returnerar samma resultat som formeln =XI2.FÖRD(x; n; FALSK), dvs. sannolikhetstäthet XI2 distributioner.
I exempelfil på grafikbladet beräkning ges gammafördelning likvärdig alfa*beta Och
GRUNDLÄGGANDE LAGAR FÖR DISTRIBUTION AV KONTINUERLIGA Slumpmässiga VARIABLER
Hnormalfördelningslagen och dess betydelse i sannolikhetsteorin. Logaritmiskt normallag. Gammafördelning. Exponentiell lag och dess användning i tillförlitlighetsteori, köteori. Lika lag. distribution. Elevfördelning. Fisher distribution.
1. Normalfördelningslag (Gauss lag).
Sannolikhetstätheten för en normalfördelad stokastisk variabel uttrycks med formeln:
 . (8.1)
. (8.1)
På fig. 16 visar fördelningskurvan. Det är symmetriskt om
Ris. 16 Fig. 17
poäng (maxpoäng). Vid minskning ökar ordinatan för maxpunkten oändligt. I detta fall är kurvan proportionellt tillplattad längs x-axeln, så att dess area under grafen förblir lika med ett(Fig. 17).
Normalfördelningslagen är mycket utbredd i praktiska problem. Lyapunov var den första som förklarade orsakerna till den stora spridningen av normalfördelningslagen. Han visade att om en stokastisk variabel kan betraktas som summan av ett stort antal små termer, så är distributionslagen för denna stokastiska variabel under tillräckligt allmänna förhållanden nära normal, oavsett vilka lagarna för fördelningen av individuella termer är. . Och eftersom praktiskt taget slumpmässiga variabler i de flesta fall är resultatet av ett stort antal olika orsaker, visar sig normallagen vara den vanligaste fördelningslagen (för mer om detta, se kapitel 9). Låt oss ange de numeriska egenskaperna hos en normalfördelad stokastisk variabel:
Således representerar parametrarna och i uttryck (8.1) för normalfördelningslagen den matematiska förväntan och standardavvikelsen för en stokastisk variabel. Med hänsyn till detta kan formel (8.1) skrivas om enligt följande:
 .
.
Denna formel visar att normalfördelningslagen helt bestäms av den matematiska förväntan och variansen hos en slumpvariabel. Således karaktäriserar den matematiska förväntan och varians helt en normalfördelad stokastisk variabel. Det säger sig självt att i det allmänna fallet, när distributionslagens karaktär är okänd, räcker inte kunskap om den matematiska förväntan och variansen för att fastställa denna distributionslag.
Exempel 1. Beräkna sannolikheten för att en normalfördelad stokastisk variabel uppfyller olikheten.
Lösning. Med hjälp av egenskap 3 för sannolikhetstätheten (kapitel 4, avsnitt 4) får vi:
 .
.
 ,
,
var finns Laplace-funktionen (se bilaga 2).
Låt oss göra några numeriska beräkningar. Om vi sätter , under villkoren i exempel 1, då
Det sista resultatet betyder att med en sannolikhet nära ett (), går en stokastisk variabel som följer normalfördelningslagen inte utöver intervallet ![]() . Detta uttalande kallas tre sigma regler.
. Detta uttalande kallas tre sigma regler.
Slutligen, om , , så kallas en slumpvariabel fördelad enligt normallagen med sådana parametrar en standardiserad normalvariabel. På fig. 18 visar en graf över sannolikhetstätheten för detta värde  .
.
2. Logaritmisk normalfördelning.
En slumpvariabel sägs ha en log-normalfördelning (förkortad lognormalfördelning) om dess logaritm är normalfördelad, dvs
där värdet har en normalfördelning med parametrar, .
Densiteten för lognormalfördelningen ges av följande formel:
 ,
.
,
.
Den matematiska förväntan och variansen bestäms av formlerna
 ,
,
 .
.
Fördelningskurvan visas i fig. 19.
Log-normalfördelningen förekommer i ett antal tekniska problem. Den ger fördelningen av partikelstorlekar vid krossning, fördelningen av innehållet av grundämnen och mineraler i magmatiska bergarter, fördelningen av mängden fisk i havet m.m. Det finns i alla
de problem där logaritmen för den aktuella kvantiteten kan representeras som summan av ett stort antal oberoende enhetligt små kvantiteter:
 ,
,
dvs.  , där är oberoende.
, där är oberoende.