The inverse Pythagorean theorem. Lesson "theorem, the reverse of the Pythagorean theorem." II. Checking homework

Lesson Objectives:

Educational: formulate and prove the Pythagorean theorem and the converse of the Pythagorean theorem. Show their historical and practical significance.

Developing: develop attention, memory, logical thinking students, the ability to reason, compare, draw conclusions.

Educational: to cultivate interest and love for the subject, accuracy, the ability to listen to comrades and teachers.

Equipment: Portrait of Pythagoras, posters with tasks for consolidation, textbook "Geometry" grades 7-9 (I.F. Sharygin).

Lesson plan:

I. Organizing time- 1 min.

II. Examination homework– 7 min.

III. introduction teachers, historical background - 4-5 min.

IV. Formulation and proof of the Pythagorean theorem - 7 min.

V. Formulation and proof of the theorem converse to the Pythagorean theorem - 5 min.

Fixing new material:

a) oral - 5-6 minutes.
b) written - 7-10 min.

VII. Homework - 1 min.

VIII. Summing up the lesson - 3 min.

During the classes

I. Organizational moment.

II. Checking homework.

p.7.1, No. 3 (at the board according to the finished drawing).

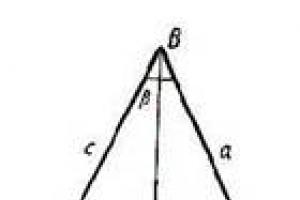
Condition: The height of a right triangle divides the hypotenuse into segments of length 1 and 2. Find the legs of this triangle.

BC = a; CA=b; BA=c; BD = a 1 ; DA = b 1 ; CD = hC

Additional question: write the ratios in right triangle.

item 7.1, No. 5. Cut the right triangle into three triangles similar to each other.

Explain.

ASN ~ ABC ~ SVN

(draw students' attention to the correct recording of the corresponding vertices of similar triangles)

The truth will remain eternal, as soon as a weak person knows it!

And now the Pythagorean theorem is true, as in his distant age.

It is no coincidence that I began my lesson with the words of the German novelist Chamisso. Our lesson today is about the Pythagorean theorem. Let's write the topic of the lesson.

Before you is a portrait of the great Pythagoras. Born in 576 BC. Having lived for 80 years, he died in 496 BC. Known as an ancient Greek philosopher and teacher. He was the son of the merchant Mnesarchus, who often took him on his trips, thanks to which the boy developed curiosity and a desire to learn new things. Pythagoras is a nickname given to him for his eloquence (“Pythagoras” means “persuasive speech”). He himself did not write anything. All his thoughts were recorded by his students. As a result of the first lecture he gave, Pythagoras acquired 2,000 students who, together with their wives and children, formed a huge school and created a state called “Great Greece”, which is based on the laws and rules of Pythagoras, revered as divine commandments. He was the first to call his reasoning about the meaning of life philosophy (philosophy). He was prone to mystification and demonstrative behavior. Once Pythagoras hid underground, and learned about everything that was happening from his mother. Then, withered like a skeleton, he declared in the public assembly that he had been in Hades, and showed amazing awareness of earthly events. For this, the touched inhabitants recognized him as God. Pythagoras never cried and was generally inaccessible to passions and excitement. He believed that he comes from a seed that is better compared to human. The whole life of Pythagoras is a legend that has come down to our time and told us about the most talented man of the ancient world.

The formulation of the Pythagorean theorem is known to you from the course of algebra. Let's remember her.

In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.

However, this theorem was known many years before Pythagoras. For 1500 years before Pythagoras, the ancient Egyptians knew that a triangle with sides 3, 4 and 5 is rectangular and used this property to build right angles when planning land and constructing buildings. In the oldest Chinese mathematical and astronomical work that has come down to us, “Zhiu-bi”, written 600 years before Pythagoras, among other sentences related to a right triangle, the Pythagorean theorem is also contained. Even earlier, this theorem was known to the Hindus. Thus, Pythagoras did not discover this property of a right-angled triangle; he was probably the first to generalize and prove it, to transfer it from the field of practice to the field of science.

Since ancient times, mathematicians have been finding more and more proofs of the Pythagorean theorem. There are over a hundred and fifty known. Let's recall the algebraic proof of the Pythagorean theorem, known to us from the course of algebra. (“Mathematics. Algebra. Functions. Data analysis” G.V. Dorofeev, M., “Bubblehead”, 2000).

Invite students to remember the proof for the drawing and write it on the board.

(a + b) 2 \u003d 4 1/2 a * b + c 2 b a

a 2 + 2a * b + b 2 \u003d 2a * b + c 2

a 2 + b 2 = c 2 a a b

The ancient Hindus, to whom this reasoning belongs, usually did not write it down, but accompanied the drawing with only one word: “Look.”

Let us consider in a modern presentation one of the proofs belonging to Pythagoras. At the beginning of the lesson, we remembered the theorem on ratios in a right triangle:

h 2 \u003d a 1 * b 1 a 2 \u003d a 1 * c b 2 \u003d b 1 * c

We add the last two equalities term by term:

b 2 + a 2 \u003d b 1 * c + a 1 * c \u003d (b 1 + a 1) * c 1 \u003d c * c \u003d c 2; a 2 + b 2 = c 2

Despite the apparent simplicity of this proof, it is far from being the simplest one. After all, for this it was necessary to draw a height in a right-angled triangle and consider similar triangles. Please write down this proof in your notebook.

What is the inverse of this theorem? (... if the condition and conclusion are reversed.)

Let's now try to formulate the theorem, the reverse of the Pythagorean theorem.

If in a triangle with sides a, b and c the equality with 2 \u003d a 2 + b 2 is true, then this triangle is right-angled, and the right angle is opposite to side c.

(Proof of the inverse theorem on a poster)

ABC, BC = a,

AC = b, BA = c.

a 2 + b 2 = c 2

Prove:

ABC - rectangular,

Proof:

Consider a right triangle A 1 B 1 C 1,

where C 1 \u003d 90 °, A 1 C 1 \u003d a, A 1 C 1 \u003d b.

Then, according to the Pythagorean theorem, B 1 A 1 2 \u003d a 2 + b 2 \u003d c 2.

That is, B 1 A 1 \u003d c A 1 B 1 C 1 \u003d ABC on three sides of ABC - rectangular

C = 90°, which was to be proved.

1. According to the poster with ready-made drawings.

Fig.1: find AD if BD = 8, BDA = 30°.

Fig. 2: find CD if BE = 5, BAE = 45°.

Fig.3: find BD if BC = 17, AD = 16.

2. Is a triangle right-angled if its sides are expressed by numbers:

What are the triples of numbers in the last two cases called? (Pythagorean).

No. 9. The side of an equilateral triangle is equal to a. Find the height of this triangle, the radius of the circumscribed circle, the radius of the inscribed circle.

№ 14. Prove that in a right triangle the radius of the circumscribed circle is equal to the median drawn to the hypotenuse and equal to half of the hypotenuse.

Item 7.1, pp. 175-177, analyze Theorem 7.4 (generalized Pythagorean theorem), No. 1 (oral), No. 2, No. 4.

What new did you learn at the lesson today? …………

Pythagoras was first and foremost a philosopher. Now I want to read you a few of his sayings, which are relevant in our time for you and me.

• Do not raise dust on the path of life.
• Do only what in the future will not upset you and will not force you to repent.
• Never do what you do not know, but learn everything you need to know, and then you will lead a quiet life.
• Don't close your eyes when you want to sleep without understanding all your actions on the previous day.
• Learn to live simply and without luxury.

Consideration of topics school curriculum with the help of video lessons is a convenient way to study and assimilate the material. Video helps to focus students' attention on the main theoretical points and not to miss important details. If necessary, students can always listen to the video lesson again or go back a few topics.

This 8th grade video lesson will help students learn new theme by geometry.

In the previous topic, we studied the Pythagorean theorem and analyzed its proof.

There is also a theorem which is known as the inverse Pythagorean theorem. Let's consider it in more detail.

Theorem. A triangle is right-angled if it satisfies the equality: the value of one side of the triangle squared is the same as the sum of the other two sides squared.

Proof. Suppose we are given a triangle ABC, in which the equality AB 2 = CA 2 + CB 2 is true. We need to prove that angle C is 90 degrees. Consider a triangle A 1 B 1 C 1 in which angle C 1 is 90 degrees, side C 1 A 1 is equal to CA and side B 1 C 1 is equal to BC.

Applying the Pythagorean theorem, we write the ratio of the sides in the triangle A 1 C 1 B 1: A 1 B 1 2 = C 1 A 1 2 + C 1 B 1 2 . By replacing the expression with equal sides, we get A 1 B 1 2 = CA 2 + CB 2.

We know from the conditions of the theorem that AB 2 = CA 2 + CB 2 . Then we can write A 1 B 1 2 = AB 2 , which implies that A 1 B 1 = AB.

We have found that in triangles ABC and A 1 B 1 C 1 three sides are equal: A 1 C 1 = AC, B 1 C 1 = BC, A 1 B 1 = AB. So these triangles are congruent. From the equality of triangles it follows that the angle C is equal to the angle C 1 and, accordingly, is equal to 90 degrees. We have determined that triangle ABC is a right triangle and its angle C is 90 degrees. We have proved this theorem.

The author then gives an example. Suppose we are given an arbitrary triangle. The dimensions of its sides are known: 5, 4 and 3 units. Let's check the statement from the theorem converse to the Pythagorean theorem: 5 2 = 3 2 + 4 2 . If the statement is correct, then the given triangle is a right triangle.

In the following examples, the triangles will also be right-angled if their sides are equal:

5, 12, 13 units; the equality 13 2 = 5 2 + 12 2 is true;

8, 15, 17 units; the equation 17 2 = 8 2 + 15 2 is true;

7, 24, 25 units; the equation 25 2 = 7 2 + 24 2 is true.

The concept of the Pythagorean triangle is known. It is a right triangle whose side values ​​are integers. If the legs of the Pythagorean triangle are denoted by a and c, and the hypotenuse b, then the values ​​of the sides of this triangle can be written using the following formulas:

b \u003d k x (m 2 - n 2)

c \u003d k x (m 2 + n 2)

where m, n, k are any integers, and the value of m is greater than the value of n.

An interesting fact: a triangle with sides 5, 4 and 3 is also called the Egyptian triangle, such a triangle was known in ancient Egypt.

In this video tutorial, we got acquainted with the theorem, the converse of the Pythagorean theorem. Consider the proof in detail. Students also learned which triangles are called Pythagorean triangles.

Students can easily get acquainted with the topic "Theorem, the inverse of the Pythagorean theorem" on their own with the help of this video lesson.

The Pythagorean theorem says:

In a right triangle, the sum of the squares of the legs is equal to the square of the hypotenuse:

a 2 + b 2 = c 2,

• a And b- legs forming a right angle.
• With is the hypotenuse of the triangle.

Formulas of the Pythagorean theorem

• a = \sqrt(c^(2) - b^(2))
• b = \sqrt (c^(2) - a^(2))
• c = \sqrt (a^(2) + b^(2))

Proof of the Pythagorean Theorem

The area of ​​a right triangle is calculated by the formula:

S = \frac(1)(2)ab

To calculate the area arbitrary triangle area formula:

• p- semiperimeter. p=\frac(1)(2)(a+b+c) ,
• r is the radius of the inscribed circle. For a rectangle r=\frac(1)(2)(a+b-c).

Then we equate the right sides of both formulas for the area of ​​a triangle:

\frac(1)(2) ab = \frac(1)(2)(a+b+c) \frac(1)(2)(a+b-c)

2 ab = (a+b+c) (a+b-c)

2 ab = \left((a+b)^(2) -c^(2) \right)

2ab = a^(2)+2ab+b^(2)-c^(2)

0=a^(2)+b^(2)-c^(2)

c^(2) = a^(2)+b^(2)

Inverse Pythagorean theorem:

If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle. That is, for any triple positive numbers a, b And c, such that

a 2 + b 2 = c 2,

there is a right triangle with legs a And b and hypotenuse c.

Pythagorean theorem- one of the fundamental theorems of Euclidean geometry, establishing the relationship between the sides of a right triangle. It was proved by the scientist mathematician and philosopher Pythagoras.

The meaning of the theorem in that it can be used to prove other theorems and solve problems.

Additional material:

Pythagorean theorem- one of the fundamental theorems of Euclidean geometry, establishing the relation

between the sides of a right triangle.

It is believed that it was proved by the Greek mathematician Pythagoras, after whom it is named.

Geometric formulation of the Pythagorean theorem.

The theorem was originally formulated as follows:

In a right triangle, the area of ​​the square built on the hypotenuse is equal to the sum of the areas of the squares,

built on catheters.

Algebraic formulation of the Pythagorean theorem.

In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.

That is, denoting the length of the hypotenuse of the triangle through c, and the lengths of the legs through a And b:

Both formulations pythagorean theorems are equivalent, but the second formulation is more elementary, it does not

requires the concept of area. That is, the second statement can be verified without knowing anything about the area and

by measuring only the lengths of the sides of a right triangle.

The inverse Pythagorean theorem.

If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then

triangle is rectangular.

Or, in other words:

For any triple of positive numbers a, b And c, such that

there is a right triangle with legs a And b and hypotenuse c.

The Pythagorean theorem for an isosceles triangle.

Pythagorean theorem for an equilateral triangle.

Proofs of the Pythagorean theorem.

On this moment 367 proofs of this theorem have been recorded in the scientific literature. Probably the theorem

Pythagoras is the only theorem with such an impressive number of proofs. Such diversity

can only be explained by the fundamental significance of the theorem for geometry.

Of course, conceptually, all of them can be divided into a small number of classes. The most famous of them:

proof area method, axiomatic And exotic evidence(For example,

by using differential equations).

1. Proof of the Pythagorean theorem in terms of similar triangles.

The following proof of the algebraic formulation is the simplest of the proofs constructed

directly from the axioms. In particular, it does not use the concept of the area of ​​a figure.

Let ABC there is a right angled triangle C. Let's draw a height from C and denote

its foundation through H.

Triangle ACH similar to a triangle AB C on two corners. Likewise, the triangle CBH similar ABC.

By introducing the notation:

we get:

,

which matches -

Having folded a 2 and b 2 , we get:

or , which was to be proved.

2. Proof of the Pythagorean theorem by the area method.

The following proofs, despite their apparent simplicity, are not so simple at all. All of them

use the properties of the area, the proof of which is more complicated than the proof of the Pythagorean theorem itself.

• Proof through equicomplementation.

Arrange four equal rectangular

triangle as shown in the picture

on right.

Quadrilateral with sides c- square,

since the sum of two acute angles is 90°, and

the developed angle is 180°.

The area of ​​the whole figure is, on the one hand,

area of ​​a square with side ( a+b), and on the other hand, the sum of the areas of four triangles and

Q.E.D.

3. Proof of the Pythagorean theorem by the infinitesimal method.

​

Considering the drawing shown in the figure, and

watching the side changea, we can

write the following relation for infinite

small side incrementsWith And a(using similarity

triangles):

Using the method of separation of variables, we find:

More general expression to change the hypotenuse in case of increments of both legs:

Integrating this equation and using the initial conditions, we obtain:

Thus, we arrive at the desired answer:

As it is easy to see, the quadratic dependence in the final formula appears due to the linear

proportionality between the sides of the triangle and the increments, while the sum is related to the independent

contributions from the increment of different legs.

A simpler proof can be obtained if we assume that one of the legs does not experience an increment

(in this case, the leg b). Then for the integration constant we get:

According to van der Waerden, it is very likely that the ratio in general form was already known in Babylon around the 18th century BC. e.

Approximately 400 BC. e., according to Proclus, Plato gave a method for finding Pythagorean triples, combining algebra and geometry. Around 300 B.C. e. in the "Elements" of Euclid appeared the oldest axiomatic proof of the Pythagorean theorem.

Wording

The main formulation contains algebraic operations - in a right triangle, the lengths of the legs of which are equal a (\displaystyle a) And b (\displaystyle b), and the length of the hypotenuse is c (\displaystyle c), the relation is fulfilled:

An equivalent geometric formulation is also possible, resorting to the concept of area figure: in a right triangle, the area of ​​the square built on the hypotenuse is equal to the sum of the areas of the squares built on the legs. In this form, the theorem is formulated in Euclid's Principia.

Inverse Pythagorean Theorem- the statement about the rectangularity of any triangle, the lengths of the sides of which are related by the relation a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). As a consequence, for any triple of positive numbers a (\displaystyle a), b (\displaystyle b) And c (\displaystyle c), such that a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), there is a right triangle with legs a (\displaystyle a) And b (\displaystyle b) and hypotenuse c (\displaystyle c).

Proof

At least 400 proofs of the Pythagorean theorem have been recorded in the scientific literature, which is explained both by the fundamental value for geometry and by the elementary nature of the result. The main directions of proofs are: algebraic use of the ratios of elements triangle (such, for example, is the popular similarity method), area method, there are also various exotic proofs (for example, using differential equations).

Through similar triangles

Euclid's classical proof aims to establish the equality of the areas between the rectangles formed by dissecting the square above the hypotenuse with the height from the right angle with the squares above the legs.

The construction used for the proof is as follows: for a right triangle with a right angle C (\displaystyle C), squares over the legs and and squares over the hypotenuse A B I K (\displaystyle ABIK) height is being built C H (\displaystyle CH) and the beam that continues it s (\displaystyle s), dividing the square above the hypotenuse into two rectangles and . The proof is aimed at establishing the equality of the areas of the rectangle A H J K (\displaystyle AHJK) with a square over the leg A C (\displaystyle AC); the equality of the areas of the second rectangle, which is a square above the hypotenuse, and the rectangle above the other leg is established in a similar way.

Equality of the areas of a rectangle A H J K (\displaystyle AHJK) And A C E D (\displaystyle ACED) established through the congruence of triangles △ A C K ​​(\displaystyle \triangle ACK) And △ A B D (\displaystyle \triangle ABD), the area of ​​each of which is equal to half the area of ​​squares A H J K (\displaystyle AHJK) And A C E D (\displaystyle ACED) respectively, in connection with the following property: the area of ​​a triangle is equal to half the area of ​​a rectangle if the figures have a common side, and the height of the triangle to the common side is the other side of the rectangle. The congruence of triangles follows from the equality of two sides (sides of squares) and the angle between them (composed of a right angle and an angle at A (\displaystyle A).

Thus, the proof establishes that the area of ​​the square above the hypotenuse, composed of rectangles A H J K (\displaystyle AHJK) And B H J I (\displaystyle BHJI), is equal to the sum of the areas of the squares above the legs.

Proof of Leonardo da Vinci

The area method also includes the proof found by Leonardo da Vinci. Let there be a right triangle △ A B C (\displaystyle \triangle ABC) right angle C (\displaystyle C) and squares A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG) And A B H J (\displaystyle ABHJ)(see picture). In this proof on the side H J (\displaystyle HJ) the latter, a triangle is constructed to the outside, congruent △ A B C (\displaystyle \triangle ABC), moreover, reflected both relative to the hypotenuse and relative to the height to it (that is, J I = B C (\displaystyle JI=BC) And H I = A C (\displaystyle HI=AC)). Straight C I (\displaystyle CI) splits the square built on the hypotenuse into two equal parts, since triangles △ A B C (\displaystyle \triangle ABC) And △ J H I (\displaystyle \triangle JHI) are equal in construction. The proof establishes the congruence of quadrilaterals C A J I (\displaystyle CAJI) And D A B G (\displaystyle DABG), the area of ​​each of which, on the one hand, is equal to the sum of half the areas of the squares on the legs and the area of ​​the original triangle, on the other hand, to half the area of ​​the square on the hypotenuse plus the area of ​​the original triangle. In total, half the sum of the areas of the squares over the legs is equal to half the area of ​​the square over the hypotenuse, which is equivalent to the geometric formulation of the Pythagorean theorem.

Proof by the infinitesimal method

There are several proofs using the technique of differential equations. In particular, Hardy is credited with a proof using infinitesimal leg increments a (\displaystyle a) And b (\displaystyle b) and hypotenuse c (\displaystyle c), and preserving the similarity with the original rectangle, that is, ensuring the fulfillment of the following differential relations:

By the method of separation of variables, a differential equation is derived from them c d c = a d a + b d b (\displaystyle c\ dc=a\,da+b\,db), whose integration gives the relation c 2 = a 2 + b 2 + C o n s t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). Application of initial conditions a = b = c = 0 (\displaystyle a=b=c=0) defines a constant as 0, which results in the assertion of the theorem.

The quadratic dependence in the final formula appears due to the linear proportionality between the sides of the triangle and the increments, while the sum is due to the independent contributions from the increment of different legs.

Variations and Generalizations

Similar geometric shapes on three sides

Important geometric generalization Pythagorean theorems were given by Euclid in the Elements, passing from the areas of squares on the sides to the areas of arbitrary similar geometric shapes: the sum of the areas of such figures built on the legs will be equal to the area of ​​​​a figure similar to them, built on the hypotenuse.

The main idea of ​​this generalization is that the area of ​​such a geometric figure is proportional to the square of any of its linear dimensions and, in particular, to the square of the length of any side. Therefore, for similar figures with areas A (\displaystyle A), B (\displaystyle B) And C (\displaystyle C) built on legs with lengths a (\displaystyle a) And b (\displaystyle b) and hypotenuse c (\displaystyle c) accordingly, there is a relation:

Since according to the Pythagorean theorem a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), then it is done.

In addition, if it is possible to prove without using the Pythagorean theorem that for the areas of three similar geometric figures on the sides of a right triangle, the relation A + B = C (\displaystyle A+B=C), then using the reverse of the proof of Euclid's generalization, we can derive the proof of the Pythagorean theorem. For example, if on the hypotenuse we construct a right triangle congruent to the initial one with area C (\displaystyle C), and on the legs - two similar right-angled triangles with areas A (\displaystyle A) And B (\displaystyle B), then it turns out that the triangles on the legs are formed as a result of dividing the initial triangle by its height, that is, the sum of two smaller areas of the triangles is equal to the area of ​​the third, thus A + B = C (\displaystyle A+B=C) and, applying the relation for similar figures, the Pythagorean theorem is derived.

Cosine theorem

The Pythagorean theorem is special case a more general cosine theorem that relates the lengths of the sides in an arbitrary triangle:

where is the angle between the sides a (\displaystyle a) And b (\displaystyle b). If the angle is 90°, then cos ⁡ θ = 0 (\displaystyle \cos \theta =0), and the formula simplifies to the usual Pythagorean theorem.

Arbitrary triangle

There is a generalization of the Pythagorean theorem to an arbitrary triangle, operating solely on the ratio of the lengths of the sides, it is believed that it was first established by the Sabian astronomer Sabit ibn Kurra. In it, for an arbitrary triangle with sides, an isosceles triangle with a base on the side c (\displaystyle c), the vertex coinciding with the vertex of the original triangle, opposite the side c (\displaystyle c) and angles at the base equal to the angle θ (\displaystyle \theta ) opposite side c (\displaystyle c). As a result, two triangles are formed, similar to the original one: the first one with sides a (\displaystyle a), the lateral side of the inscribed isosceles triangle far from it, and r (\displaystyle r)- side parts c (\displaystyle c); the second is symmetrical to it from the side b (\displaystyle b) with a party s (\displaystyle s)- the relevant part of the side c (\displaystyle c). As a result, the relation is fulfilled:

which degenerates into the Pythagorean theorem at θ = π / 2 (\displaystyle \theta =\pi /2). The ratio is a consequence of the similarity of the formed triangles:

Pappus area theorem

Non-Euclidean geometry

The Pythagorean theorem is derived from the axioms of Euclidean geometry and is invalid for non-Euclidean geometry - the fulfillment of the Pythagorean theorem is equivalent to the postulate of Euclidean parallelism.

In non-Euclidean geometry, the relationship between the sides of a right triangle will necessarily be in a form different from the Pythagorean theorem. For example, in spherical geometry, all three sides of a right triangle, which bound the octant of the unit sphere, have length π / 2 (\displaystyle \pi /2), which contradicts the Pythagorean theorem.

Moreover, the Pythagorean theorem is valid in hyperbolic and elliptic geometry, if the requirement that the triangle is rectangular is replaced by the condition that the sum of two angles of the triangle must be equal to the third.

spherical geometry

For any right triangle on a sphere with radius R (\displaystyle R)(for example, if the angle in the triangle is right) with sides a , b , c (\displaystyle a,b,c) the relationship between the sides is:

This equality can be derived as a special case of the spherical cosine theorem, which is valid for all spherical triangles:

Where ch (\displaystyle \operatorname (ch) )- hyperbolic cosine. This formula is a special case of the hyperbolic cosine theorem, which is valid for all triangles:

Where γ (\displaystyle \gamma )- an angle whose vertex is opposite to a side c (\displaystyle c).

Using the Taylor series for the hyperbolic cosine ( ch ⁡ x ≈ 1 + x 2 / 2 (\displaystyle \operatorname (ch) x\approx 1+x^(2)/2)) it can be shown that if the hyperbolic triangle decreases (that is, when a (\displaystyle a), b (\displaystyle b) And c (\displaystyle c) tend to zero), then the hyperbolic relations in a right triangle approach the relation of the classical Pythagorean theorem.

Application

Distance in two-dimensional rectangular systems

The most important application of the Pythagorean theorem is to determine the distance between two points in a rectangular system coordinates: distance s (\displaystyle s) between points with coordinates (a , b) (\displaystyle (a,b)) And (c , d) (\displaystyle (c,d)) equals:

For complex numbers the Pythagorean theorem gives a natural formula for finding the modulus complex number - for z = x + y i (\displaystyle z=x+yi) it is equal to the length