Ministry of Education and Science Samara region

State autonomous educational institution additional vocational education(advanced training) of specialists

SAMARA REGIONAL INSTITUTE FOR PROFESSIONAL DEVELOPMENT

AND RETRAINING OF EDUCATIONAL WORKERS

On advanced training courses

According to WB IOCH

"Methodological features of teaching to solve problems with a parameter in the context of the transition to new educational standards"

(15.06 - 19.06.2015)

Designing a multi-level system of tasks with a topic parameter:

"Derivative"

Performed:

Valieva F.G.,

mathematic teacher

GBOU secondary school them. M.K. Ovsyannikova

With. Isakla

Samara

2015

EXPLANATORY NOTE

Full name (full name)

Valieva Fanuzya Galimzyanovna

Place of work

GBOU secondary school them. M.K. Ovsyannikova village of Isakly,

Isaklinsky district, Samara region

Job title

Mathematic teacher

Item

Mathematics

Class

Goals:

implementation of the requirements of the Federal State Educational Standard LLC when studying the topic: "Derivative"
Generalization and systematization of knowledge and methods of activity on the topic "Derivative"; formation of skills to solve problems with parameters.
Development of research and cognitive activity.

The concept of spiritual and moral development and education of the personality of a citizen of Russiais methodological basis development and implementation of the federal state educational standard general education.

Federal state educational standard for basic general education about school course mathematics.

The standard is based onsystem-activity approach.

The standard establishes requirements for the results of mastering the basic educational program basic general education:

personal;

metasubject ;

subject .

Tasks:

- educational: analyze and comprehend the text of the task, independently identify and formulate a cognitive goal, reformulate the condition, build a logical chain of reasoning, critically evaluate the answer received, conscious and arbitrary construction of a speech statement, choice of the most effective way problem solving, problem formulation and formulation, hypotheses and their justification, semantic reading;

- developing: goal-setting, plan their activities depending on specific conditions; reflection of the methods and conditions of action, control and evaluation of the process and results of activities, self-regulation,through problem solving, to develop the creative and mental activity of students, intellectual qualities: the ability to "vision" the problem, evaluative actions, independence, flexibility of thinking;

- educational: sense formation, the ability to listen and enter into a dialogue, to participate in a collective discussion of problems, to cultivate responsibility and accuracy.

Tasks with parameters - these are non-standard tasks, i.e.unusual both in formulation and content, and in methods of solution. The role of suchtasks, their importance and benefits for development logical thinking, intuition,creative abilities of students, the formation of their high mathematicalcultures are very large. It is known that educators face seriousmethodological problems in teaching to solve such problems, despite the presence,enough a large number tutorials and journal articles. The reason for this is quite obvious: the main strategy mathematics education at school, this is the development of skills and abilities to solve a certain set of standard problems, most of them related to the technique of algebraic transformations. Equations (inequalities) with parameters refer to a different type of tasks - tasks for the solution of which, first of all, the ability to carry out - sometimes quite branched - logical constructions and research is necessary.

Solving problems with parameters requires research, even if this word is not mentioned in the problem statement. The mechanical application of formulas is not enough, it is necessary to understand the patterns, the ability to analyze a specific case based on known common properties object, consistency and consistency in the solution, the ability to combine the considered particular cases into a single result. This is due to the difficulties that students have in solving such problems.

At present, the idea of combining learning to solve problems with learning to design them has become quite widespread. By constructing a task, we will understand the process of creating a new task. The construction of the problem is based on the ability to compose a square trinomial. In this case, various techniques are used: analogy, variation of coefficients square trinomial, variation of a new variable, variation of task requirements. More complex functions can act as coefficients and a new variable. Thus, you can use such a square trinomial, which will help in organizing the repetition of more complex functions: exponential, logarithmic, trigonometric. On the one hand, you need to know the properties of the square trinomial, and on the other hand, the properties of the function are repeated, thereby achieving a combination of the problem.

The choice of a problem with parameters for teaching their solution and design can be explained by the following circumstances:

when solving problems with parameters, repetition occurs, and as a result, a deeper, more solid assimilation of program issues;

solving problems with parameters expands the mathematical horizons, gives new approaches to solving problems;

there is a development of mathematical, logical thinking, the ability to analyze, compare, generalize;

skills for research work are acquired;

assistance in preparing for exams;

there is a formation of such personality traits as diligence, purposefulness, perseverance, willpower, accuracy.

Formed UUD within the framework of the Federal State Educational Standard when solving problems with parameters:

Stages of problem solving

Formed UUD

Condition Analysis(introduction of letters)

goal setting;
highlighting material information;
formulation of the problem and forecasting of solutions;
abstraction;
analogy;
classification (typology);
symbolic actions.

Schematic record of the condition of the problem in the form of a table, diagram, graphwith introduced letters

planning;
systematization;
symbolic actions;
modeling.

Building a Model(search for an analogue, attraction of a known law from mathematics or physics)

creation of a method for solving zalachi;
condition adjustment;
modeling in graphical form.

Solving equations, systems, etc.(search for the unknown)

analysis and identification of material information;
derivation of consequences;
building a chain of reasoning;
development and testing of hypotheses;
model transformation.

Model interpretation(verification and evaluation of solutions, roots)

analysis;
derivation of consequences;
specification;
symbolic action (interpretation).

Study(generalization of the problem or a method for solving it for modified conditions, other approaches to solving)

analysis;
synthesis;
search for analogues;
building a chain of reasoning;
the ability to concisely convey content;
skill diagrams, symbols, models;
creation of ways to solve problems of a search, creative nature.

Reflection

meaning formation;
planning;
control;
correction;
grade;
volitional self-regulation;
readiness for self-development, for self-education;
the ability to independently determine the goals of their training;
set and formulate new tasks for yourself;
develop the motives and interests of their educational activities.

Multi-level task system

The basis of the teaching methodology based on a multi-level system of tasks is the gradual development of the blocks of its matrix. The main feature of this technique is that at each level, i.e. when mastering the corresponding column of the matrix, the student each time encounters all three types of learning situations that arise when solving problems.

A multi-level system of tasks for each topic of the course is formed using its matrix representation, by highlighting a ranked list basic elements the content of education and the basic tasks corresponding to them, on the one hand, and the levels of learning that reflect the ability to solve familiar, modified and unfamiliar tasks, on the other.

Such a matrix of the topic task system contains 3 rows corresponding to three types of learning situations that arise when solving problems, andN columns reflecting the number of basic tasks of the topic. Such a tabular (matrix) representation of the system of tasks of the topic helps to carry out full-fledged filling at each level of its mathematical and activity (formation of UUD) components and thereby implementcriteria for subject and activity completeness (meaning cognitive UUD) formed system learning objectives. At the same time, if the basic tasks in the system play the role of a kind of integrators of the subject-content component, then when designing and implementing the learning process, a similar role should be played by universal tasks. learning activities (common methods and methods of activity) in selected situations.

Educational activity in solving problems included in the first line of the matrix is of a reproductive nature (such general educational actions as classification, summing up under a concept, deriving consequences, actions, building a logical chain of reasoning, proof, etc.) are used. The tasks involved are different.explicit connections between the data and the required (known and unknown) elements. The student identifies (recognizes familiar tasks in a number of similar ones), reproduces the studied methods or algorithms of actions, applies the acquired knowledge in practical terms for some known class of tasks and receives new information based on the application of the learned activity model.

When solving problems of the second line, reproductive educational activity combined with a reconstructive one, in which patterns of activity are not simply reproduced from memory, but are reconstructed under somewhat modified conditions (here such general educational actions are manifested as the selection and formulation of a cognitive goal, the search and selection of the necessary information, sign-symbolic actions, including math modeling, structuring knowledge).

Finally, when solving problems of the third line, educational activity is of a research creative nature. The student must be able to navigate in new situations and develop fundamentally new programs of action (put forward a hypothesis, check: substantiate or refute, put forward a new one, etc., carry out research activities). Solving the problems of the corresponding block requires the student to have an extensive fund of proven and quickly deployed algorithms; the ability to quickly recode information from a sign-symbolic form to a graphic one and, conversely, from a graphic to a sign-symbolic one; systemic vision of the course. At the same time, it does not just involve the use of old algorithms in new conditions and an increase in technical complexity, but is distinguished by the non-obviousness of the application and combination of the studied algorithms. The tasks of this level have a complicated logical structure and are characterized by the presencelatent connections between the data and the elements you are looking for. Such tasks are usually offered as the most difficult at entrance exams to universities with high requirements for the mathematical preparation of applicants and in tasks 17, 18, 20, 21 of the KIM USE.

Multilevel system of tasks on the topic "Derivative"

№ p/p

Task name

Task type

Derivative calculation by definition.

MOH

Finding derivatives of sums, products, private functions

MOH

Investigation of the monotonicity of a function

function increases along the whole number line?

MOH

At what values of the parameter function decreasing for all values ?

Find the set of all numbers a, for each of which the functionf(x) = sin 2 x – 8(a + 1) sinx + (4 a 2 + 8 a – 14) xis increasing on the entire real line and has no critical points.

Finding extremum points

has one fixed point?

MOH

Determine at what value of the parameter function maximum is 9

For what values of the parameter a the functionf(x) = (a 2 – 3 a + 2) (cos 2 – sin 2 + (a – 1) x + sin1 has no critical points?

Finding the largest and smallest values continuous function on an interval and differentiable on an interval

Find out for what values of the parameterA smallest function valuey = x 2 -12 x + a on the segment is zero.

MOH

At what value of the parameter smallest function value equals

At what values of the parameter function takes values less than 5 for any

Complete exploration and plotting

3+3x2

MOH

At what value of the parameter a is the minimum of the function f(x) = ax 2 - 6ax + a 2 - 9 is equal to 1?

The equation of the tangent to the graph of a function at a given point

At what values of the parameter straight is tangent to the graph of the function ?

MOH

At what values of the parameter tangent to function graph cuts off from the first quarter an isosceles triangle with area

At what values of the parameter tangent to the graph of the function drawn at the points of its intersection with the axis, form an angle

Application of the derivative to solving problems in geometry, physics and economics

What should be the sides of a rectangle with a perimeterPto maximize its area?

MOH

The window has the shape of a rectangle bounded on top by a semicircle (Figure 3). The perimeter of the window is P. Determine the radius of the semicircle R, at which the area of the window is the largest.

A picture of height a is hung on the wall in such a way that its lower edge is h units above the observer's eye level. At what distance x from the wall should the observer be in order for the viewing angle of the painting to be the largest (Figure 7a)?

Solutions

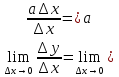
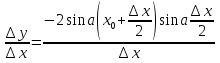
Solution :

1. The function f(x) decreases for all values of x if the derivative

f′(x) = 6ax 2 + 18ax + 30a = 6a(x 2 + 3x + 5)< 0

for all x.

2. Hence we find that a< 0.

3 . Answer: a (–∞; 0).

Find the set of all numbers a, for each of which the function f (x) \u003d sin 2x - 8 (a + 1) sinx + (4a 2 + 8a - 14) x is increasing on the entire real line and does not have critical points.

1. For any fixed a, this function is differentiable at every point on the real line.

2. Since the function f(x) is increasing, the inequality f′(x) ≥ 0 must hold at each point x.

3. Since, moreover, f(x) has no critical points, then for any x the inequality f′(x) ≠ 0 must hold.

4. Thus, if the function satisfies the condition of the problem, then for all x the inequality f (x) > 0 must be satisfied.

5. On the other hand, if the inequality f′(x) > 0 holds for all x, then the function obviously has no critical points and is increasing.

6. Find the derivative of this function:

f′( x) = 2 cos 2 x – 8( a + 1) cosx + 4 a 2 + 8 a – 14.

Now the problem can be reformulated as follows: find all values of the parameter a, for each of which, for any x, the inequality

cos 2x – 4(a + 1) cos x + 2a 2 + 4a – 7 > 0.(1)

7. Given that cos 2x = 2 cos 2 x – 1, and setting cos x = t, where –1 ≤ t ≤ 1, we rewrite inequality (1) as follows:

2t 2 – 1 – 4(a + 1)t + 2a 2 + 4a – 7 > 0,

t 2 – 2(a + 1)t + a 2 + 2a – 4 > 0. (2)

8. Denoting the function on the left side of inequality (2) by ϕ(t), we give a new formulation of the original problem: find all values of a, for each of which the least value of the function ϕ(t) on the interval [–1; 1] is positive.

9. The derivative ϕ′(t) = 2t – 2(a + 1) vanishes at t 0 = a + 1.

10. The smallest value of the function ϕ(t) on the interval [–1; 1] is:

ϕ (–1) = a 2 + 4a – 1,Ifa + 1 ≤ –1;

ϕ (a + 1) = -5,If –1 < a + 1 < 1;

ϕ(1) = a 2 – 5 if a + 1 ≥ 1.

11. Since the smallest value of the function ϕ(t) on the segment [–1; 1] must be positive, then the values of the parameter a satisfying the condition of the problem belong to two intervals: a ≤ –2 and a ≥ 0.

12. If a ≤ –2, then the desired values of the parameter a satisfy the inequality a 2 + 4a – 1 > 0.

13. If a ≥ 0, then the desired values of the parameter a satisfy the inequality a 2 – 5 > 0.

14. Consequently, the set of desired values a is the union of solutions of two systems of inequalities:

(3)

a ≥ 0

A 2 -5 > 0 (4)

15. The set of solutions to system (3) is the interval –∞< a < –2 –√5 , а множество решений системы (4)- промежуток a >√5 .

16. Answer: a (–∞; –2 –√5) (√5; +∞).

1. Since this function is differentiable on the entire real line, the critical points of the function f(x) are those points at which the derivative f′(x) = 0.

2. In this case, we have f (x) =(a – 1)(a – 2) (–sin+ (a – 1).

3. Obviously, if a = 1, then f (x) = 0 for any x R, i.e.

for a given function, each point x R is critical.

4. Assume that a 1. Then the equation f (x) = 0 takes the form

(a - 2) sin = 2. (1)

It follows that if |a – 2|< 2, т. е. если a (0; 1) (1; 4),

then equation (1) has no roots and, therefore, for the indicated values of a, the function f(x) has no critical points.

5 . Answer: a (0; 1) (1; 4).

The smallest value of the numerator and highest value the denominator is reached at different meanings X. Therefore, to find the smallest value of a function, it is convenient to use the derivative. Let us rewrite the inequality in the form

Wheret=3- cos 2 x, t

Find the smallest value of the functionf( t) = , on the segment. Since the derivativef "( t) = negative attThatfdecreases and takes the smallest value att=3, f name = f(3) = .

Answer:a

What is the smallest natural k for which the equation x 3+3x2 – 45x + k = 0 has exactly one root?

1. Construct a sketch of the graph of the function y 1 = x 3 + 3x 2 – 45x and determine the smallest natural value of k for which this graph intersects the line y 2 = –k at exactly one point.

2. a) D(y 1 ) = R;

boo 1 / = 3x 2 + 6x - 45; 1 / in the intervals (–∞; –5), (–5; 3) and (3; +∞) is illustrated in Fig. 1. In fig. 2 is a schematic representation of the graph of the function y 1 .

3. Obviously, this equation has a unique solution if –k > 175 or –k< –81, т. е. k < –175 или k >81. The smallest natural value of k is 82.

4. Answer: k = 82.

At what value of the parameter a is the minimum of the function f(x) = ax2 – 6ax + a2 – 9 equal to 1?

1. f′(x) = –6x 2 + 6x + 12.

2. y′ = 0 for x 1 = 2.

6. Answer: a = 2.

At what value of the parameter a is the minimum of the function f(x) = –2x 3 + 3x 2 + 12x + 4a is 1?

For what values of the parameter a is the line y=ax-2 tangent to the graph of the function y=1+ln⁡ x?

At what values of the parameter a the tangent to the graph of the function y=a-x^2 cuts off an isosceles triangle with an area of 9/32 from the first quarter

because , by condition the tangent must intersect the function inquarters means. An isosceles triangle is a right triangle so the other angles are equal, Butwhence the tangent takes the form the point of contact of the tangent with the graph along the x-axis is equal to . according to the formula tangent to the graph since the area of a triangle should be , That because quarter.Where

At what values of the parameter a, the tangents to the graph of the function y=4x^2-|a|x, drawn at the points of its intersection with the x-axis, form an angle of 60° between them

What should be the sides of a rectangle with perimeter P for its area to be maximum?

Literature

Azarov A.I., Barvenov S.A., Fedosenko V.S.Methods for solving problems with parameters. Mathematics for high school students. Minsk: "Aversev", 2003.

V.S. Vysotsky, Tasks with parameters for preparing for the exam

Gorshtein P.I., Polonsky V.B., Yakir M.S. Tasks with parameters. - K.: RIA "Text"; MP "OKO", 1992. -290 p.

Kachalova G. A. On the need to include the content-methodical line "Problems with parameters" in training module"Fundamentals of Mathematics" //Matterł yMię dzynarodowejNaukowi- PraktycznejkonferencjiPostę pó wwnauce. Nowepoglą dy, problemy, innowacje. 29.07.2012. - 31.07.2012. część 2. - Łodź, 2012. - S. 67–70.

Kozko A. I., Panferov V. S., Sergeev I. N., Chirsky V. G. USE 2011. Mathematics. Task C5. Tasks with a parameter / Ed. A. L. Semenova and I. V. Yashchenko. - M.: MTsNMO, 2011.-144 p.

Rodionov E.M. Solving problems with parameters. M.: MP "Rus-90", 1995

1. Task.
At what values of the parameter a the equation ( a - 1)x 2 + 2x + a- 1 = 0 has exactly one root?

1. Decision.
At a= 1 equation has the form 2 x= 0 and obviously has a single root x= 0. If a No. 1, then this equation is quadratic and has a single root for those values of the parameter for which the discriminant of the square trinomial zero. Equating the discriminant to zero, we obtain an equation for the parameter a 4a 2 - 8a= 0, whence a= 0 or a = 2.

1. Answer: the equation has a single root at a O(0; 1; 2).

2. Task.
Find all parameter values a, for which the equation has two different roots x 2 +4ax+8a+3 = 0.
2. Decision.
The equation x 2 +4ax+8a+3 = 0 has two distinct roots if and only if D = 16a 2 -4(8a+3) > 0. We get (after reduction by a common factor of 4) 4 a 2 -8a-3 > 0, whence

2. Answer:

a O (-Ґ ; 1 -

C 7 2

) AND (1 +

C 7 2

; Ґ ).

3. Task.
It is known that
f 2 (x) = 6x-x 2 -6.
a) Graph the function f 1 (x) at a = 1.
b) At what value a function graphs f 1 (x) And f 2 (x) have a single common point?

3. Solution.
3.a. Let's transform f 1 (x) in the following way
The graph of this function a= 1 is shown in the figure on the right.
3.b. We immediately note that the function graphs y = kx+b And y = ax 2 +bx+c (a No. 0) intersect at a single point if and only if the quadratic equation kx+b = ax 2 +bx+c has a single root. Using View f 1 of 3.a, we equate the discriminant of the equation a = 6x-x 2 -6 to zero. From Equation 36-24-4 a= 0 we get a= 3. Doing the same with equation 2 x-a = 6x-x 2 -6 find a= 2. It is easy to verify that these parameter values satisfy the conditions of the problem. Answer: a= 2 or a = 3.

4. Task.
Find all values a, under which the set of solutions of the inequality x 2 -2ax-3a i 0 contains the segment .

4. Solution.
The first coordinate of the vertex of the parabola f(x) = x 2 -2ax-3a is equal to x 0 = a. From properties quadratic function condition f(x) i 0 on the interval is equivalent to the totality of three systems
has exactly two solutions?

5. Decision.
Let's rewrite this equation in the form x 2 + (2a-2)x - 3a+7 = 0. This is a quadratic equation, it has exactly two solutions if its discriminant is strictly greater than zero. Calculating the discriminant, we get that the condition for having exactly two roots is the fulfillment of the inequality a 2 +a-6 > 0. Solving the inequality, we find a < -3 или a> 2. The first of the inequalities is obviously solutions in natural numbers does not have, and the smallest natural solution of the second is the number 3.

5. Answer: 3.

6. Task (10 cells)
Find all values a, for which the graph of the function or, after obvious transformations, a-2 = | 2-a| . The last equation is equivalent to the inequality a i 2.

6. Answer: a O , and does not depend on the sign of the discriminant. Let's make schematic drawings (for D>0)

https://pandia.ru/text/78/525/images/image020_10.jpg" width="624" height="209 src=">

For each of the three cases a), b), c) the smallest value of the function f(t) = t2-8at+7a2

on the segment is achieved, respectively, at the points at x = 1, x = 2a, x = 1/4. Then the question to answer is the solution of the totality of three systems:

1≤4a 1/4<4а<1 4а<1/4

f(1)<0 или f(4а)<0 или f(1/4)<0

a≥1/4 1/16<а<1/4 а≤1/16

1 - 8a + 7a2<0 или 16а2 – 32а2 + 7а2<0 или 1/16 – 2а + 7а2<0.

Answer: 1/28<а<1.

Test tasks

1). For what values of the parameter a do the graphs of the functions y = 2x – a and y = (a + 1)x2 + 1 intersect at only one point?

2). Find all values of the parameter a for which the graphs of the functions y = (a + 5)x2 - 1 and

y \u003d (3a + 15) x - 4 do not have common points?

3). For what values of the parameter a does the equation (a +4)x2 +6x –1 = 0 have a unique solution?

4). For what values of the parameter a does the equation (2a + 8) x2 - (a + 4) x + 3 = 0 have a unique solution?

5). For what values of the parameter a does the equation have more than one solution?

a) (a + 6)x2 - 8x + a \u003d 0

b) a (2a + 4) x2 - (a + 2) x - 5a - 10 = 0.

6). Find all values of the parameter k for which the curve y = x2 + kx + 4 touches the x-axis.

7). What is the smallest integer value of the parameter k for the square trinomial

(k–2)x2+8x + k+4 is positive for all real values of x?

8). The numbers x, y, and are such that x + y = a -1, x2 + y2 = 5a2 - 3a + 0.5. At what values of the parameter a does the product xy take on the maximum value?

9). The numbers x, y, and are such that x + y = a +1, xy = a2 - 3a + 4. For what values of the parameter

and the sum x2 + y2 takes the maximum value?

10). Find the largest and 1 smallest value of the function y \u003d 2x2 - 2ax + on the segment

eleven). Find the largest value of the square trinomial 1 - (a - 2) x - x2 on the segment

12). At what values of the parameter a is the smallest value of the function y = x2 + (a + 4) x + 2a + 3 on the segment equal to -4?

13). At what values of the parameter a is the smallest value of the function y \u003d x2 - (a + 2) x + a2 on the segment [-1; 1] equal to 4?

14). At what values of the parameter a is the maximum value of the function

f (x) \u003d - (1 / a) x + (7 / a) 3-x - 3a2 on the segment [-1; 0] is negative?

Answers to the test task

1) a=-2, a=-1, a=0.

2) –19/3<а≤-5.

3) a=-4, a=-13.

5) a) -8<а<-6 и -6<а<2

b) a=-2; -1/40 0.

10) If a<-2, то наименьшее значение функции при х=-1 и равно 3+2а, наибольшее значение функции при х=1 и равно 3–2а;

if -2≤a<0, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=1 и равно 3–2а;

if 0≤a<2, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=-1 и равно 3+2а;

if a≥2, then the smallest value of the function at x= 1 and equal to 3–2a, the largest value of the function at x=-1 and equal to 3+2a;

11) If a≤0, then -6a2-a+2, if 0<а<8/5, то 2- 6а +а2/4, если а ≥8/5, то 19а-6а2 -14

13) a=-2 or a=(1+√21)/2

14) |a|>(7√3)/12.

Location of the roots of a square trinomial

Consider a number of typical problems related to the location of the roots of the square trinomial ax2 + bx + c. We will carry out all the reasoning assuming a > 0. If a<0,то рассуждения проводятся аналогично.

Task number 1.

Under what conditions are both roots quadratic equation ax2+bx+c =0 (not necessarily distinct) greater than some given number k?

Solution.

We construct schematic graphs of the function of a square trinomial y= ax2+bx+c, where x1 and x2 satisfy the conditions: x1>k, x2>k. Let f(x)=ax2+bx+c. Graph y= f(x) either crosses the OX axis (D>0) or touches it (D=0). Then it is necessary to fulfill the condition: х>к, y(к)>0. If a< 0 условие: х1>k, x2>k are determined by the system of inequalities:

https://pandia.ru/text/78/525/images/image023_20.gif" width="14" height="86">

Fig.4

Task 11. Find all values of the parameter a for which all roots of the equation

x2–6ax+2–2a+9a2 = 0 more than 3.

Solution.

If the required condition is met, the following positions of the parabola are possible, which is the graph of the function f(x)= x2–6ax+2–2a+9a2

Fig.5

Let's solve the system of inequalities:

https://pandia.ru/text/78/525/images/image026_8.jpg" align="left" width="324" height="239 src=">

It is enough to fulfill the condition: y(k)<0, если а >0.When a<0, y(к) > 0.

Rice. 6

Task 12. Find all values of the parameter a for which 1 lies between the roots of the equation x2–2ax+3–4a+2a2=0.

Solution.

Since the leading coefficient is positive, it suffices to satisfy the condition f(1)<0, где f(х)=х2–2ах+3–4а+2а2

4–6a+2a2<0, 1<а<2.

Answer: 1<а<2

Task number 3. Under what conditions exactly one root of the quadratic equation ax2 + bx + c = 0, which has different roots, lies on the interval (k, e)?

Let us schematically construct graphs y = ax2 + bx + c according to the condition of this problem for a > 0.

https://pandia.ru/text/78/525/images/image028_8.jpg" width="623" height="246 src=">

Solve the inequality: f(1) f(2)<0.

(a2+8a+7)(a2+14a+16)<0

7-√33< а<-7; -7+√33<а<-1.

Answer: -7-√33< а<-7; -7+√33<а<-1.

Task 14. Find all values of the parameter a for which the equation 2cos(2x)+2asin(x)+a-1=0 has a unique solution on the interval (-π/2;0).

Solution.

2cos(2x)+2a sinx+a-1=0

2(1–2 sin2х)+ 2a sinx+a–1=0

4 sin2х–2а sinx –a–1=0

Let sinx=t Since -π/2<х<0, то -1< t <0

Find those values of the parameter a for which the equation 4t2– 2at–a–1=0 has a unique solution on the interval (-1; 0).

The equation 4t2– 2at–a–1=0 has a unique solution on the interval (-1; 0) if:

1). D \u003d 0 D / 4 \u003d (a + 2) 2 D \u003d 0 for a \u003d -2.

2). Consider the function f(t)= 4t2– 2at–a–1

We construct a schematic graph of the function y=f(t)

https://pandia.ru/text/78/525/images/image030_16.gif" width="14" height="50 src=">

f(0) f(1) ≤0 a≤-3; a≥-1

Answer: a≤-3; a≥-1; a=-2.

Task number 4. Under what conditions do both roots (not necessarily different) of the quadratic equation ax2 + bx + c lie on the segment [k; e]. Consider under the condition a>0. Let there be a function f(x)= ax2+bx+c

https://pandia.ru/text/78/525/images/image032_14.gif" width="14" height="110"> D≥0

k≤ ho≤ e

Task 15. Find those values of the parameter a for which all the roots of the equation

х2- 2(а–3)х–а +3=0 lie in the interval (-3; 0).

Solution.

Provided that at least one root exists, the graph of the function f (x) \u003d x2- 2 (a-3) x-a + 3 can be schematically located in one of two ways

https://pandia.ru/text/78/525/images/image034_12.gif" width="14" height="110"> D≥0 4(а – 3)(а – 2) ≥0

3<хо<0 3<а – 3 <0 1,2<а≤2.

f(-3) >0 5а – 6>0

f(0) >0 -а+3>0

Equation sin x - 1 + a = sin x - 2 . sin x − 2 sin x − 3 Solution. Setting t = sin x, we reduce the equation to the form at2 − 5at + 6a − 1 = 0. If a = 0, then there are no solutions. For a = 0 and under the condition a ∈ (−∞; −4] ∪ (0; +∞) √ 2 + 4a we obtain the roots of the equation t1,2 = 5a ± 2aa . Since the vertex of the parabola f (t) = at2 − 5at + 6a − 1 is located at the point tв = 2 , 5 the condition |t|1 for the smallest of the roots will be satisfied if the function has different signs at the ends of the segment [−1; 1]: f (−1) f (1) 0 or (2a−1)(12a−1) 0. The solution to the last 1 inequality is the interval a ∈ 12 ;1 .2 √ a2 Answer: If a ∈ 12 ;2: x = (−1)n arcsin 5a− 2a +4a +πn, n∈Z, 1 1 there are no solutions for other a. Problem 6.7 For which values of the parameter a the function f (x) = 8ax − a sin 6x − 7x − sin 5x is increasing on the entire real axis and has no critical points? Solution. The function f (x) is differentiable for any value of a and f (x) = 8a − 6a cos 6x − 7 − 5 cos 5x. The problem can be reformulated as follows: for which a the inequality 6a cos 6x + 5 cos 5x< 8a − 7 справедливо для любого x? Так как последнее неравенство должно выполняться для любого значения x, оно должно быть справедливо и для x = 0, от- куда 6a + 5 < 8a − 7 или a >6. Considering now that 6a cos 6x + 5 cos 5x 6|a| +5< 8a − 7, приходим к выводу, что при a >6 the inequality is valid for any x. Answer: a > 6. Tasks for independent decision Problem 6.8. (SGAU) Depending on the values of the parameter a, solve the equation cos4 x − (a + 2) cos2 x √ a − 3 = 0. − Answer: If a ∈ [−3; −2] : x = arccos a + 3 + πk, k ∈ Z, if a ∈ [−3; −2] : no solutions. Problem 6.9. (SGAU) Depending on the values of the parameter a, solve the equation sin4 x + cos4 x + sin 2x + a = 0. 61 √ Answer: If a ∈ − 3 ; 2: x = 1 (−1)k arcsin(1− 2a−3) + πk, 2 1 2 3 ; 1: no solutions. if a ∈ − 2 2 k ∈ Z, Problem 6.10. (SGAU) For what values of the parameter a does the equation (a2 +8a+16)(2−2 cos x− sin2 x)+(32+2a2 +16a)(cos x−1)+3a+10=0 solutions? Answer: a< − 10 ; −3 < a < −2. 3 Задача 6.11. (СГАУ) При каких значениях параметра a урав- нение loga−2 17 + cos x − sin x = 3 8 имеет решение? √ 2 3 Ответ: a ∈ 2 5 ; 3 ∪ 3; 2 + 26 . 2 Задача 6.12. (СГАУ) При каких значениях параметра a урав- нение loga+1 25 + cos x − 2 sin x = 3 8 2 имеет решение? √3 37 Ответ: a ∈ − 1 ; 0 ∪ 0; 2 − 1 . 2 Задача 6.13. (ЕГЭ) При каких значениях параметра a значение выражения 2+cos x·(3 cos x+a sin x) не равно нулю ни при каких значениях x? √ √ Ответ: a ∈ −2 10; 2 10 . Задача 6.14. (ЕГЭ) При каких значениях параметра a значение выражения 3 + sin x · (2 sin x + a cos x) будет равно −1 хотя бы при одном значении x? √ √ Ответ: a ∈ −∞; −4 6 ∪ 4 6; +∞ . Задача 6.15. (ЕГЭ) При каких значениях параметра a сумма loga (sin x + 2) и loga (sin x + 3) будет равна единице хотя бы при одном значении x? Ответ: a ∈ [ 2; 12 ]. Задача 6.16. (СГАУ) При каких значениях параметра α систе- ма 4 sin x · sin y · cos(x + y) − 0,5 = 0 x−y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. 62 Ответ: Если α = 2πn: x = ±π 6 + π(k+n) π y = ±6 + π(k−n); если α = π+2πn: x = ±π 3 + π + π(k+n) 2 y = ±π 3 − π + π(k−n), 2 n, k ∈ Z. Задача 6.17. (СГАУ) При каких значениях параметра α систе- ма 2 sin x · cos y · sin(x − y) + 0,25 = 0 x+y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. Ответ: Если α = π +2πn: x = (−1)k+1 π + π + π (2n+k) 2 12 4 2 k π + π + π (2n−k); y = (−1) 12 4 2 если α = − 2 π +2πn: x = (−1)k π − π + π (2n+k) 12 4 2 y = (−1) k+1 π − π + π (2n−k), 12 4 2 n, k ∈ Z. Задача 6.18. (СГАУ) При каких значениях параметра a нера- венство √ 2 2 (sin x − cos x) − a + 7 log 2a+34 15 <0 35 выполняется для любых значений x? 1 Ответ: a ∈ (−17; −12) ∪ 2 ; 3 . Задача 6.19. (СГАУ) При каких значениях параметра a нера- венство √ log 3−2a 3 sin x + 3 3 cos x − 2a − 12 >0 23 28 holds for any values of x? Answer: a ∈ (−∞; −23) ∪ (−10; −9). Problem 6.20. Depending on the values of the parameter a, solve the inequality cos x 2 − a2 . Answer: |a| √ : x ∈ R, 1 1<|a| √3: x ∈ arccos(2−a2)+2πk; π− arccos(2−a2)+2πk , |a|>3: no solutions. k∈Z Problem 6.21. For what values of the parameter a does the equation tg x (a + 1) tg2 x − 2 cos x + a = 0 have no solutions? Answer: a -3; a 1.63 Tutorial PROBLEM WITH PARAMETERS Compiled by: Efimov Evgeny Alexandrovich Kolomiets Lyudmila Vadimovna Computer typesetting and layout E.A. Efimov Samara State Aerospace University named after Academician S.P. Queen. 443086, Samara, Moscow highway, 34. - RIO Samara State Aerospace University named after Academician S.P. Queen. 443086, Samara, Moscow highway, 34.